NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Tiro oblicuo) |
|

|
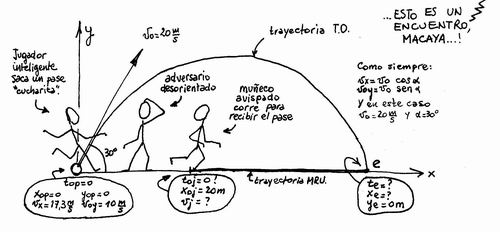
| NMS c5.13* - Un jugador de fútbol ejecuta un tiro libre, lanzando la pelota con un ángulo de 30º con la horizontal y a una velocidad de 20 m/s. Un segundo jugador corre con velocidad constante para alcanzar la pelota, partiendo al mismo tiempo que ella, desde 20 m más adelante de la posición de disparo. Despreciando el tiempo que necesita para arrancar, calcular con qué velocidad debe correr para alcanzar la pelota cuando ésta llega al suelo. |
|
Aquí tenemos un típico "problema de pizarrón". Pekerman diría "calculemos cuánto tarda la pelota en retornar al césped y, si utilizamos ese tiempo para calcular la velocidad del jugador, entonces, aplicando logaritmos en ambos miembros y trigonometría para la velocidad inicial, dividimos por la aceleración media, e integrando el logaritmo el problema sale fácil". Es un método, no lo vamos a negar. E inteligente también. Pero yo creo que la física es una ciencia democrática, para todo el mundo, no sólo para inteligentes y superdotados. Creo que la física es también método. Y veremos cómo ese método resuelve todos los problemas. Como siempre, empezamos por un esquema. |
|
|
 |
|
|
| El esquema nos va a ser de mucha utilidad. ¿Cuántas ecuaciones describen este problema? C-u-a-t-r-o. Porque hay dos movimientos: un TO y un MRU (el del muñeco). Cada TO se describe con tres ecuaciones y cada MRU con una. (Este cuestionamiento es importante porque nunca vamos a poder escribir una ecuación si no estamos dispuestos a hacerlo). Para armar estas ecuaciones horarias basta con tener a mano los modelos: |
|
|
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
|
|
|
y reemplazar las constantes (to , xo , yo , vx , voy , y g). Acá están, finalmente, las cuatro ecuaciones: |
|
|
| jugador |
x = 20 m + vj . t |
|
| pelota |
x = 17,3 m/s . t
y = 10 m/s . t – 5 m/s² . t²
vy = 10 m/s – 10 m/s² . t |
|
|
|
Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado |
| Lo que sigue es obvio: ahora que tenemos las herramientas, LAS USAMOS. Es decir, les pedimos que hablen del único punto en el que puede haber interés: el punto e, el encuentro entre el muñeco y la pelota. (En este caso, la tercera ecuación de la pelota -la de velocidad vertical- no aporta nada útil, pues no nos piden averiguar con qué velocidad llega la pelota. Pero si no nos apiolamos de ésto, no hay drama; la usamos igual, no molesta). |
|
|
 |
xe = 20 m + vj . te
xe = 17,3 m/s . te
0 m = 10 m/s . te – 5 m/s² . te² |
[1]
[2]
[3] |
|
|
|
| ¡Penal! ¡Hemos encontrado un sistema de tantas ecuaciones como incógnitas! ¡Un empujoncito y es gooool! (Yo sabía que íbamos a llegar a esta instancia... siempre leo NO ME SALEN). Acá terminó la física, el resto es álgebra. Te hago una de las 679 resoluciones posibles (para que no llores). |
|
 |
De la ecuación [3] despejamos te y calculamos. Fijate que la [3] es una cuadrática, así que usamos la salvadora: |
|
|
|
|
|
(o si te animás despejás directamente, ya que es una cuadrática incompleta: no tiene término independiente). Lo hagas como lo hagas vas a obtener dos valores de te; uno de ellos tiene que ser 0, ya que no te olvides que las ecuaciones son tontas: lo que vos le estás preguntando realmente es "en qué instante(s) la altura de la pelota es cero", y bueno, ella responde. Coeficientes: c = 0, b = 10 m/s, a = – 5 m/s².
te1 = 0 s (este no sirve)
te2 = 2 s (éste es el nuestro)
Con ese valor para el instante de encuentro vamos a la ecuación [2]
xe = 17,3 m/s . 2 s
xe = 34,6 m
Y ahora, con los dos valores que hallamos, nos vamos a la ecuación [1]
34,6 m = 20 m + vj . 2 s
y despejamos vj |
|
|
| |
vj = 7,3 m/s |
(¡Bravo, Macaya!) |
|
|
|
| |
|
|
| * Este jercicio pertenecía a la guía de problemas de la materia Fisica que se usó hasta el año 2002. Se trataba del ejercicio 5.8 y es una pena que lo hayan quitado de la guía de problemas actual. |
|
|
|
| |
|
|
| DESAFIO: El muñeco sale 0,5 segundos después que la pelota. (Obvio que va a tener que correr más, pero ¿cuánto?). |
|
 |
| |
| Permitida la reproducción parcial, final o libre de este material didáctico. No apto para machete. Prohibida la comercialización. Las transgresiones a esta disposición serán penalizadas con 24 clases de "El ser es y el no ser no es" de Introducción a la Filosofía.
Sólo se permite su reproducción citando la fuente. Todos los derechos reservados. Agradezco la colaboración del eminente filósofo Javier J. Casal que ne comunicó una errata. Última actualización ago-06. Buenos Aires, Argentina. |
|
|
|

