NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, fuerzas elásticas)
|
|

|
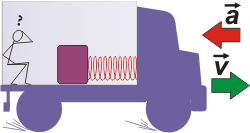
No me salen 5.04 * - Una caja de 30 kg se encuentra apoyada en el piso (sin rozamiento) y unida a la pared delantera de un camión por medio de un resorte de constante elástica k = 60.000 N/m. En un momento, cuando el camión esta frenando con una aceleración de 6 m/s², un operario dentro del camión ve que la caja está quieta respecto del piso del mismo. ¿Cómo se encuentra el resorte en ese momento?
|
a) comprimido 3 mm
b) comprimido 3 cm
c) estirado 3 mm
d) no se puede saber si esta estirado o comprimido
e) estirado 3 m
f) no está estirado ni comprimido |
 |
|
|
|
*Este es un problema hermoso formó parte del examen final del curso tomado en Ciudad Universitaria en julio de 2007. Tuvo un 50% de respuestas acertadas. A mí me gustó por dos motivos: su sencillez y la justeza del enunciado.
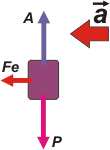
Como todo problema de dinámica que se precie... hay que comenzar por un DCL |
|
|
|
En la dirección vertical aparece el peso de la caja y el apoyo sobre el piso. Está claro que esas fuerzas no juegan ningún papel importante en este problema. Y también agregué una fuerza elástica, Fe, hacia la izquierda... como si el resorte estuviese comprimido.
No es necesario saber -a priori- si está comprimido o estirado... o incluso relajado sin deformación. Yo planteo la fuerza para donde me guste, y luego serán las ecuaciones las que dictaminarán si la fuerza apuntaba efectivamente para ese lado, o si era para el otro, o si valía cero... y lo mismo sobre la deformación del resorte, ¿ok? |
|
|
|
Fijate que en este DCL te dibujé (y bien grande) la aceleración de la caja. Ese dato es fundamental y solamente lo captaron quienes leyeron el enunciado atentamente. Decía: ve que la caja está quieta respecto del piso del mismo. O sea: la caja y el camión tienen la misma aceleración. Podría no serlo, porque el resorte no es un cuerpo rígido. Pero es la misma aceleración, porque lo indica el enunciado. Vamos a las ecuaciones (sólo del eje x)
Fe = m . a
Esa igualdad es de tipo vectorial. No sólo son iguales los módulos de ambos miembros, también lo son la dirección y el sentido. Y como la aceleración apunta hacia la izquierda, la fuerza elástica también debe hacerlo. Eso me indica que el resorte está comprimido. Para saber cuánto le pedimos ayuda a Hooke.
Fe = k . Δx
La Ley de Hooke siempre la uso en su versión "módulo" ya que habitualmente el sentido de los vectores (y sus signos) los discutimos aparte, a la hora del DCL. Ya sabemos que el resorte tiene que estar comprimido, ahora vamos a saber cuánto. Igualamos esas dos ecuaciones y despejamos Δx...
m . a = k . Δx
Δx = m . a / k
|
|
|
|
|
|
|
|
|
| Tenés decenas de variaciones de este ejercicio en esta guía de problemas. Por ejemplo el 1.3, 1.4, 1.11, 1.13, 1.19, 2.9, 2.23 y Ad20. |
|  |
| |
| DESAFIO: ¿Cuánto vale la deformación del resorte justo en el instante en que el camión comienza a frenar si viajaban a 108 km/h? |
|
| Algunos derechos reservados.
Se permite su reproducción (a todo color) citando la fuente. Última actualización jul-07. Buenos Aires, Argentina. |
|
|
|

