DINAMICA, dN1.07, fisica online, ejercicios resueltos

home

más de dinámica

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)

¡no me salen!

NMS 1.7- Un péndulo cuelga en reposo del techo de un coche de ferrocarril, detenido en una vía horizontal. Si el tren arranca con aceleración constante, ¿qué ocurre con el péndulo, si se lo coloca en una posición donde permanece sin oscilar? ¿Cómo hallar, observando el péndulo, la aceleración del tren?

Este es un problema muy bonito. Voy a hacer dos DCL, el de la izquierda cuando el tren está en reposo y el de la derecha cuando todo el conjunto, tren, vagón, y péndulo, están acelerando. Tal vez no puedas predecir cómo debe ser el segundo DCL, yo, sí, porque tengo un poco más de experiencia, aunque es bastante intuitivo. De todos modos lo importante es que entiendas el razonamiento hasta el final y te cerciores de que el DCL del tren acelerado no podía ser de otra manera.

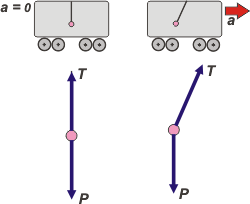Indudablemente el que nos interesa es el segundo DCL, aquél que representa las fuerzas que obran sobre el péndulo cuando el vagón está acelerado. Observá que no han aparecido nuevas fuerzas. Las únicas dos que actúan son: P, la fuerza con que la Tierra solicita al péndulo, y T, la fuerza que ejerce la cuerda que, por supuesto debe tener la misma dirección que la cuerda.

De ése DCL va a salir la solución del problema. Debemos aplicar ahora la ley de Newton, ΣF = m a

Pero hay un problema: las fuerzas no son codireccionales, son oblicuas entre sí. Debemos hacer una descomposición. Voy a elegir (a propósito) un SR con una coordenada horizontal (la misma dirección de la aceleración) y la otra vertical. El peso no hay que descomponerlo, coincide con la dirección vertical. Sí, en cambio, T.

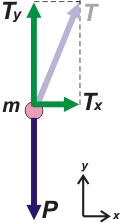Y ahora aplicamos la 2da ley por separado para cada uno de los ejes. Empecemos con la dirección horizontal

ΣF_x = m a_x

hay una sola fuerza en esa dirección; y a_x no es otra que la aceleración del vagón

T_x = m a

Ahora vamos con la dirección vertical

ΣF_y = m a_y

T_y – P = 0

T_y = m g

Pareciera que no ganamos demasiado... pero tratemos de ver si T_x y T_y , no estan por casualidad, realacionados de alguna manera.

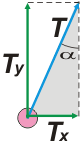Mirá el triangulito que quedó formado y que sombreé en gris. Es rectángulo, no cabe duda. El ángulo α no es otro que el ángulo de inclinación de la cuerda. T_x y T_y son los catetos de ese triángulo y T es la hipotenusa. Entonces...

T_x = T sen α

T_y = T cos α

Si metemos esta información en las ecuaciones de Newton tal como las habíamos dejado, quedan:

T sen α = m a

T cos α = m g

Ahora dividamos miembro a miembro esas dos ecuaciones... mirá lo que queda:

tg α = a / g

a = g . tg α

¡Apareció la solución! Fijate, con sólo observar el ángulo de inclinación de la cuerda se puede conocer la aceleración del vagón. Ya que g es una constante cuyo valor es conocido, valía... mmm... Conviene tener una escuadra y una calculadora, claro, pero eso es otra historia.

DISCUSION: la primer pregunta es obvia: ¿tiene las unidades correctas este resultado? Sí, tiene unidades de aceleración ya que es el producto entre g que es una aceleración (10 m/s²) y tg α, que como toda función trigonométrica es adimensional, no tiene unidades. Vamos bien. ¿Y tiene sentido físico el resultado? Y... parece que sí, fijate, si α valiera cero, tg α = 0, estamos en el primer caso y ya sabíamos que ahí la cuerda colgaba vertical. Si α crece tg α también crece, o sea cuanto más acelerado esté el vagón más inclinada estará la cuerda. Parece lógico. ¿Cuánto tendría que valer la aceleración del vagón para que α valiera 90º?

DESAFIO: Resulta que ahora el péndulo vuelve a la vertical y sabiamente deducís que el vagón está detenido o avanzando a velocidad constante. Por otro lado te consta que el camino va siempre por una llanura y que no hay ningún desnivel, ni el más mínimo. De pronto observás que el péndulo se inclina no hacia adelante ni hacia atrás... sino hacia un costado ¿te animarías a dar una explicación para ese fenómeno?