NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
rozamiento
|
|

|
d2.15- Un hombre quiere mover una caja de
10 kg que está apoyada sobre el piso de un vagón
en reposo. Para eso necesita hacer una fuerza
de 5 kgf. El vagón está ahora acelerado y el
hombre tiene ahora que hacer una fuerza de
3 kgf para mover la caja. ¿Qué aceleración lleva
el vagón?
|
| ¡Un ejercicio hermoso! Espero que lo disfrutes. La primera parte es bien sencilla. Acá va el DCL, un poco caracterizado. |
|
|
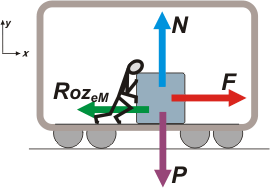 |
En este caso el vagón y el tío están quietos (en realidad deberíamos decir: no están acelerados, ¡pero quién puede preocuparse por la diferencia!). De modo que ninguna fuerza tira para su lado más que su opuesta.
La fuerza que hace el hombre, F, es la que se necesita para mover la caja, por lo tanto es igual a la fuerza de rozamiento estática máxima, RozeM, el resto lo ponemos directamente en las ecuaciones, ¿dale? |
|
|
| |
F — RozeM = 0 |
[1] |
| |
N — P = 0 |
[2] |
| y además sabemos que |
|
| |
RozeM = μe . N |
[3] |
Ahora resulta que el tipo quiere empujar la caja de nuevo, pero esta vez para ponerla en movimiento tiene que hacer menos fuerza que antes. Y el autor del problema infiere (y por eso nos pregunta) que el vagón (con caja y tipo incluído) están acelerados. Esta parte también es sencilla. No te dejes asustar, Hacé el planteo de Newton y después vemos.
La nueva fuerza que hace el tipo la voy a llamar F´. Va el nuevo DCL. |
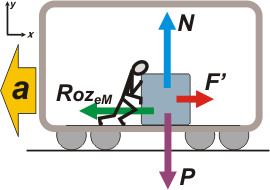 |
Qué raro para dónde dibujé la aceleración... no te preocupes, no me hagas caso. Fijate que lo único que cambié del anterior es la fuerza que hace el tipo. ¡Las otras son constantes! Pase lo que pase tienen que valer lo mismo.
El peso es constante. La fuerza que hace el piso (mientras no haya aceleración vertical ni agregado de fuerzas verticales, tiene que valer lo mismo que antes). Las superficies son las mismas... todo igual, menos la fuerza que hace el tío. |
|
| |
F´ — RozeM = m a |
[4] |
|
|
las otras ecuaciones no tengo que repetirlas, no es necesario, son iguales. Ahora las meto dodas en la licuadora y despejo a. Mirá cómo hago, hay 704 caminos diferentes y a mí se me ocurrió éste (es álgebra)
de la [1] despejo RozeM
RozeM = 50 N
eso lo meto en la [4] y despejo a
a = (F´ — RozeM) / m
|
|
|
|
O sea que apuntaba para el lado contrario a F, la dibujé bien.
DISCUSION: Primero... ¿qué puede estar haciendo el vagón? Puede estar avanzando en la dirección y sentido de x y estar frenando, ¿te cierra? O también puede estar dando marcha atrás (contra el sentido de las x) e ir cada vez más rápido. Bueno, estas son consideraciones cinemáticas en la que vos ya sos experto. O sea.
Pero todo esto me hace surgir la siguiente reflexión... ¿cómo puede la aceleración ahorrarme una fracción de la fuerza necesaria para mover la caja? ¡Te la puede ahorrar íntegra! O acaso si frenase de golpe, por ejemplo chocando contra el paragolpes, la caja ¿no saldría "despedida" hacia adelante a estrellarse con la pared delantera del vagón? ¿Acaso para hacer eso no tuvo que ponerse en movimiento (respecto del piso)? ¡Y en este caso el tipo no tuvo que mover un dedo! (salvo para sostenerse él mismo).
¿Entendés ahora? Cuando hay aceleraciones muchos fenómenos se hacen indistinguibles de las fuerzas... Mmm creo que acá tenemos un lindo problema. Pero vamos a dejarlo para más adelante. |
 |
| |
DESAFIO: Andá y busca en algún libro de física un capítulo que se llama Sistemas no-inerciales. Lee la introducción, nada más. Y por arriba. No te enrolles, es sólo para chusmear un poco y para cumplir el desafío evitando así, severas penalidades. |
|
| Algunos derechos reservados.
Se recomienda no subir a los trenes argentinos sin guantes de trabajo. Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

