 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA Y BIOFÍSICA
Ondas mecánicas
|
|

|
MOVIMIENTO OSCILATORIO EN CUERPOS Y ELÁSTICOS
|
|
Oscilaciones de los cuerpos elásticos
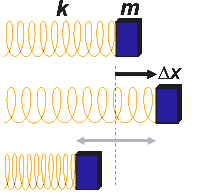
Supongamos un cuerpo elástico ideal. El mejor que podemos imaginar es un resorte ideal -sin masa- que está apoyado en una superficie horizontal sin rozamiento. Supongamos que el resorte está fijo en un extremo y en el otro tiene unido un cuerpo de masa m. |
|
|
|
Si apartamos el cuerpo una distancia Δx y lo soltamos, la fuerza restitutiva del elástico lo moverá hacia el lado opuesto y comenzará una oscilación en teoría eterna.
Se demuestra fácilmente que esa oscilación será de tipo armónica, MOA, con una amplitud igual a Δx.
¿De qué dependerá la frecuencia de la oscilación? |
|
|
|
No es difícil predecirlo... si la masa es muy grande parece lógico que la escilación resulte lenta (frecuencia baja) ya que el sistema tiene mucha inercia, le cuesta moverse. Y viceversa: si la masa es pequeña la frecuencia debe resultar alta. O sea: la frecuencia y la masa deben ser inversamente proporcionales.
Analicemos qué pasa con el elástico. Si el resorte es muy duro (constante elástica alta) parece lógico predecir un movimiento más rápido (fuerza de restitución eficaz), o sea, una frecuencia mayor. Y viceversa: si el resorte el blandito, se moverá lentamente. La constante elástica debe ser directamente proporcional a la frecuencia.
Esta otra no es tan fácil de predecir intuitivamente... pero hacé el intento: la frecuencia es independiente de la amplitud de la oscilación.
Haciendo las derivaciones algebraicas necesaria se llega a una fórmula que coincide con nuestras espectativas: |
|
|
| |
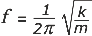 |
Puede ser que en No me salen lo veas escrito así, que es lo mismo:
f = (1/2π) (k/m)1/2 |
|
|
|
Donde f es la frecuencia de la oscilación, k es la constante elástica, y m la masa unida o asociada al elástico. La constante 1/2π proviene de la relación entre la frecuencia y velocidad angular del MCU asociado, o sea, la pulsación, ω. Es más, tal vez prefieras ver la relación de esta manera, más compacta: |
|
|
| |
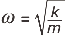 |
No te olvides de que ω = 2π . ƒ |
|
|
|
|
Todos los cuerpos elásticos que obedecen a la ley de Hooke pueden producir oscilaciones armónicas y simples. Son osciladores naturales.
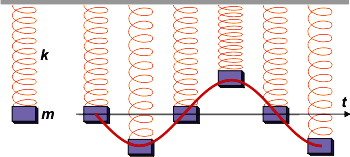
Si nuestro resorte ideal se colocase en forma vertical con el cuerpo colgando la cosa sería apenas un poco más complicada, pero el resultado sería el mismo. Si prestás atención al esquema que sigue se reforzará la idea: |
|
|
|
|
|
Veamos ahora las oscilaciones que se producen en una cuerda tensa, que bien podría ser la de un piano, un violín o un cable de alta tensión.
Nuevamente, si lo pensamos de antemano, debemos esperar que la frecuencia sea proporcional a la tensión de la cuerda (cuanto más tensa más rápido vibra, y viceversa). también parece lógico que cuanto más masiva, "pesada", sea la cuerda, menor será la frecuencia con que vibre, o sea, frecuencia y masa deben ser inversamente proporcionales. |
|
|
| |
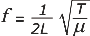 |
Puede ser que en No me salen lo veas escrito así, que es lo mismo:
f = (1/2L) (T/μ)1/2 |
|
|
|
Donde f es la frecuencia de la oscilación, L es la longitud de la cuerda, T es la tensión en la cuerda, y μ es la densidad de masa, o sea, el cociente entre la masa de la cuerda y su longitud.
μ = m / L
La diferencia fundamental con el caso anterior es que la masa que se pone en movimiento no está alojada en un extremo sino que se halla repartida uniformemente a lo largo de toda la cuerda.
Apenas más adelante, verás que las cuerdas pueden vibrar -al mismo tiempo- de varias maneras. La forma principal de movimiento (la de mayor amplitud) se llama modo fundamental y tiene la frecuencia de la que hablamos hasta ahora. Las formas secundarias se llaman armónicos, que tambiés son oscilasciones armónicas simples y se superponen unas a otras.
La fórmula general que describe todas las formas de vibración en una cuerda es ésta: |
|
|
| |
|
|
| Donde n es el número de armónico. Si n=1, se trata de la frecuencia fundamental. |
|
|
| |
|
|
| CHISMES IMPORTANTES |
|
|
-
Casi todos los sonidos son producidos por cuerpos elásticos: se mueven oscilatoriamente y, a su vez, producen otro movimiento oscilatorio en el aire al perturbarlo con su movimiento.
|
- Un péndulo simple también es un oscilador armónico simple.
|
|
|
|
 |
| PREGUNTAS CAPCIOSAS |
|
- ¿Quién fue el griego tan famoso que estudió los sonidos que producen las cuerdas?
- ¿Qué función cumplen las clavijas de la guitarra?
- ¿Un avión, puede tener una frecuencia de oscilación? ¿Y un puente? ¿Y un edificio?
|
|
| |
Algunos derechos reservados.
Se permite su reproducción citando la fuente.
Última actualización mar-13. Buenos Aires, Argentina. |
|
|
 |
 |
|
|
|

