 |
NO ME SALEN
APUNTES TEÓRICOS Y EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
Ley de Hooke
|
|

|
FUERZAS ELÁSTICAS - Ley de HOOKE
Empecemos por entender a qué se llama un cuerpo elástico: es aquel que después de deformarlo recupera por sí solo su forma original. Por ejemplo, una pelota de fútbol: uno puede aplastarla un poco ejerciendo una fuerza sobre ella (dos fuerzas, en general); a esa fuerza vamos a llamarla fuerza deformante. Cuando uno retira la fuerza deformante la pelota recupera su forma esférica.
No siempre los cuerpos elásticos se comportan en forma elástica en todas direcciones de las deformaciones como el caso de la pelota. En esta lección vamos a trabajar con cuerpos que se comportan elásticamente en una sola dirección (y en ambos sentidos). Se trata de los resortes ideales (en la jerga, simplemente: elásticos). |
 |
|
|
La elasticidad de los resortes se manifiesta en su dirección longitudinal (si lo aplastás de costado lo más probable es que te quedes sin resorte). Como te imaginás para comprimirlo o estirarlo hay que hacer fuerza en ambos extremos. Pero para entender el funcionamiento de los resortes conviene que experimentemos en un sólo extremo, así que vamos a apoyarlo contra una pared y ahí lo pegamos con poxipol 10 minutos (no tenemos todo el día). Trabajaremos sólo en el extremo libre.
Cuando una fuerza deformante actúa sobre un elástico, el elástico responde sobre el cuerpo que lo deforma con una fuerza igual y opuesta. No es que los elásticos sean vengativos, sino que, como todos los cuerpos del universo, están obligados a cumplir con la tercera Ley de la Dinámica: el Principio de Acción y Reacción. A esa fuerza que hacen los elásticos se la llama fuerza elástica. |
|
| un cuerpo plástico no recupera su forma original |
|
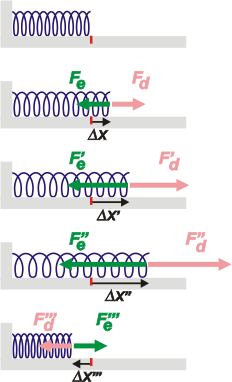 |
La fuerza que hace el elástico (la fuerza elástica, Fe) la representé en verde. Y la fuerza deformante, Fd, en rosa.
Las deformaciones (representadas con flechas negras) se miden siempre desde la posición de la última espira del resorte cuando no está perturbada por fuerzas externas (en la jerga: libre, sin carga, en reposo, y otras expresiones). Hice una marca roja en el piso indicando la posición desde la que medimos la deformación.
Cuanto mayor es la fuerza deformante más se deforma el elástico, y también mayor es la fuerza elástica. El señor Robert Hooke (1635-1703), encontró que la deformación y la fuerza elástica eran directamente proporcionales.
Fe ~ Δx
Esto vale tanto para los estiramientos o elongaciones como para las compresiones.
La fuerza elástica y la deformación del elástico siempre tienen sentidos opuestos. |
|
|
 |
| Considerando esto, y considerando que cada resorte en particular se estiraba (o se comprimía) de modo diferente a los otros sometidos a una misma fuerza deformante es obvio que el factor de proporcionalidad debía ser una constante que dependiera de cada resorte en particular. El resultado de esto es la Ley de Hooke: |
|
|
|
|
|
En la que k es la constante elástica, un valor que representa a cada resorte, que se mide en N/m o cualquier otra unidad de fuerza dividida por una unidad de longitud; y es mayor cuanto más duro y robusto sea el resorte, y menor cuanto más flacucho y debilucho sea. Más precisamente k representa la fuerza de restitución de cada resorte. |
|
|
 |
|
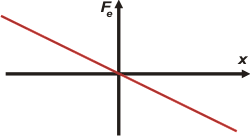
El gráfico nos muestra cómo varía la fuerza elástica en función de la posición de su última espira (respecto de la posición de relajamiento).
La zona graficada se llama período elástico (si un elástico real se lo estira o comprime mucho deja de ser un elástico y tenés que tirarlo). Bajón. |
|
|
|
| Los signos que llevan las fuerzas en las ecuaciones de Newton dependen de la discusión que realices en el DCL y del sistema de referencia que arbitrariamente elijas para resolver los ejercicios. A partir de ahí cada fuerza se comporta como un ente algebraico: no podés volver a cambiarle su signo arbitrariamente. De modo que yo te recomiendo usar la ley de Hooke sólo en módulo, Fe = k . Δx, sin el signo menos, que oscurece más que aclara, induce a error demasiadas veces. Siempre es más práctico y sencillo trabajar los sentidos de las fuerzas visualmente que analíticamente. |
|
|
| CHISMES IMPORTANTES: |
|
|
- Los resortes ideales se pueden estirar tanto como se precise y comprimir también tanto como se necesite, que siempre van a responder con fuerzas elásticas hookianas y siempre van a recuperar su longitud ideal. Todo el mundo sabe que los resortes de verdad no cumplen con ese requisito. El rango de deformaciones en el que un resorte de verdad se comporta como uno ideal se denomina período elástico. muchos resortes de verdad, aún trabajando dentro de su período elástico, se desvían considerablemente de la Ley de Hooke: no son lineales.
- En muchos textos, y en varios ejercicios de este sitio, se toma en cuenta la longitud del resorte. Y se distingue la longitud natural, o longitud sin carga, o longitud sin deformación, lo , de la longitud que adopta cuando está deformado, l; resulta obvio que Δx = l – lo.
- Como la longitud es una magnitud de fácil medida los resortes hookianos se convirtieron en el instrumento de medida de las fuerzas más confiable y seguro. El adminículo recibe el nombre de dinamómetro y consta de un par de ganchos, un extremo del resorte fijo en una regla y el otro extremo con una aguja deslizante sobre la misma regla.
- Las balanzas a resorte (dinamómetros) miden fuerzas; en cambio las balazas de brazos o platillos miden masas usando el principio de comparación. Las balanzas digitales modernas utilizan una propiedad material llamada piezoelectricidad.
|
|
 |
| dinamómetro |
| PREGUNTAS CAPCIOSAS: |
|
 |
- Si quiero pesarme en la Luna, ¿puedo usar una balanza de platillos?, ¿puedo utilizar un dinamómetro? ¿Qué adminículo utilizan los astronautas para medir masas o pesos dentro de la nave espacial?
- ¿Es posible que Robert Hooke haya disputado con Newton la paternidad de la Ley de Gravitación Universal? ¿Será Hooke uno de los gigantes?
|
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-09. Buenos Aires, Argentina. |
|
|
 |
|

