 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Gravitación)
|
|

|
| NMS 4.12 - La balanza de torsión de Cavendish. En la experiencia de Cavendish, dos esferas de 175 kg atraían a dos esferas de
0,75 kg, unidas por una varilla de 1,82 m suspendida de un hilo de 0,0034 Nm de
módulo de torsión. Si cada par esfera grande/esfera chica sus centros están separados 0,20 m y el ángulo que giró la varilla es 0,000117 radianes ¿qué valor obtuvo de G? |
|
Algunos de los datos de este ejercicio son valores históricos reales
y otros fueron dimensionados por el autor. |
|
|
Este ejercicio puede parecerte difícil, inexpugnable, atroz... de lo que no cabe duda es que se trata de un problema boludo. Y eso que los físicos consideran a este experimento uno de los 10 más brillantes de la historia de la ciencia. Primero te hago un esquema del dispositivo de Henry Cavendish... y seguimos charlando: la historia en torno a este experimento es alucinante. |
|
|
La primera hazaña del experimento es haber logrado medir la fuerza de atracción gravitatoria entre cuerpos de masas pequeñas. Se trata de una fuerza enormemente pequeña y sutil.
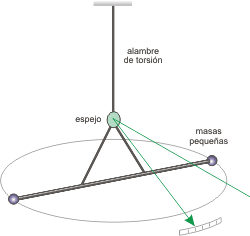
Básicamente consistió en una varilla que sujetaba horizontalmente dos masas pequeñas en los extremos, y que colgaba mediante un cable firmemente unido al techo y que se resistía a ser torcido con una fuerza contraria a la torsión (módulo de torsión) conocida. |
 |
|
|
|
Además tenía un espejo pegado en el que se hacía rebotar un rayo de luz. Si el cable -y su espejo pegado- giraban un pequeño ángulo, éste podía ser observado mediante el corrimiento del haz de luz.
Estando el dispositivo así listo, se acercaban a las esferas pequeñas otras dos mucho más grandes y se dejaban fijas. |
|
|
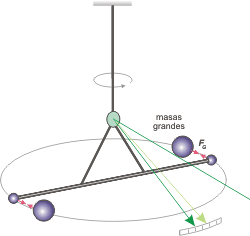
Entre cada par bola grande/bola chica se producía un fuerza de atracción gravitatoria. Esa fuerza no afectaba a las bolas grandes debido a que éstas estaban fijas. Pero a las bolas chicas les producía un pequeñísimo acercamiento que hacía torcer la varilla, el cable y el espejo. El pequeño ángulo girado producía un corrimiento de señal de luz en una escala colocada suficientemente lejos (cuanto más lejos mayor el desplazamiento y más fácil de medir).
El dispositivo utiliza dos pares de bolas, debido a que la fuerza de torsión debe ser pareja (empujar de ambos lados del cable con la misma fuerza). |
 |
|
|
|
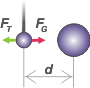
Bueno, vamos a resolver el ejercicio, todavía quedan muchas dificultades que charlar. Como la que se desplaza es la bola chica (las dos bolas chicas, en realidad) vamos a realizar el diagrama de cuerpo libre de ésta (acá representé un par visto desde arriba). |
|
|
Las fuerzas que actúan sobre ellas (cualquiera de las dos chicas) son: la fuerza gravitatoria de atracción con la bola grande más próxima, FG, y la fuerza de torsión que hace la varilla en sentido contrario, FT. |
 |
|
|
d = 0,2 m |
Las fuerzas verticales no las representé porque no interesan en este asunto y se cancelan entre ellas. La fuerza gravitatoria es igual a:
FG = G . M . m / d²
donde G es la constante de gravitación universal, M es la masa de la bola grande, m es la masa de la bola chica y d es la distancia que separa los centros de masa del par bola grande/bola chica.
La fuerza de torsión es igual a:
FT = κ . Φ / L
donde κ es el módulo de torsión, Φ es el ángulo girado (en radianes) y L es el largo de la varilla. No es frecuente que los estudiantes manejen el concepto de módulo de torsión, sobre todo si no vieron antes estática del cuerpo extenso y sus tópicos momento de una fuerza y cupla. De todos modos no es un concepto que no puedas localizar en internet y aplicarlo aún sin haberlo profundizado. Se trata de una característica de los cables y alambres equivalente a la constante elástica de los cuerpos elásticos, sólo que en vez de describir la deformación en una dimensión lineal (acortamiento o estiramiento) describe la deformación elástica de retorcimiento que, lógicamente, se mide en radianes. En nuestro alambre vale κ = 0,0034 Nm.
Igualamos ambas expresiones:
G . M . m / d² = κ . Φ / L
De ahí despejamos G y lo calculamos:
G = κ . Φ . d²/ M . m . L
G = 3,4 x 10-3 Nm . 1,17 x 10-4 . 0,04 m² / 175 kg . 0,75 kg . 1,82 m
|
|
|
| |
G = 6,67 x 10-11 Nm2kg-2 |
¡hazaña! |
|
|
|
Primera cuestión: fijate que el ángulo de 1,17 x 10-4 radianes se corresponde con 0,0067 o (grados sexagesimales), algo casi imperceptible que, amplificado por un rayo de luz que proyecta su imagen a 4 metros del espejo, nos da un desplazamiento de 0,468 milímetros... ¡Cavendish observaba los desplazamientos de la imagen con un microscopio!
Segunda cuestión: el módulo de torsión de un alambre se mide fácilmente observando el período de oscilación de la varilla en torno a una posición de equilibrio. A su vez, las posiciones de equilibrio son tan sutiles que hay que medirlas en torno a múltiples oscilaciones. Por eso Cavendish promediaba las oscilaciones de dos posiciones: una que provocaba poniendo las bolas grandes de un lado de las chicas y la otra colocándolas del lado contrario. Los cambios de emplazamiento de las bolas grandes los efectuaba operando mecánicamente el dispositivo desde afura, ya que todo se hallaba completamente cerrado a cubierto de la más mínima corriente de aire.
Tercera cuestión: Cavendish no midió G sino la masa de la Tierra que era lo que perseguía (esa historia te la cuento acá). Ese era otro dato que los físicos y astrónomos de la época buscaban afanosamente. Y Cavendish la obtuvo: MT = 5,96 x 1024 kg. Encontrado ese valor, la aceleración de la gravedad (g = 9,81 m/s2) y el radio terrestre (RT = 6,37 x 106 m), se obtiene G:
G = g . RT2 / MT
Pero no sabemos quién fue el primer físico en darse cuenta y hacer el cálculo. |
|
|
DESAFIO: ¿Cuánto vale la fuerza gravitatoria medida en el experimento? |
|
 |
| Algunos derechos, zurdos y ambidiestros reservados.
Se permite su reproducción citando la fuente. De los ambidiestros también. Última actualización may-12. Buenos Aires, Argentina. |
|
|
|

