NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC |
|

|
NMS d3.17 - Curva con peralte y rozamiento.
Acá esta, el prometido. Por un lado tenés el problema del peralte, que permite fabricar una fuerza centrípeta para girar, eso lo podés ver en el problema 1.49. Por otro lado tenés la posibilidad de doblar haciendo uso exclusivo del rozamiento en una curva horizontal, o sea no inclinada. Eso podés verlo en el problema 2.10. Acá vamos a combinar ambas fuerzas y podremos tomar curvas con mayor velocidad.
Vamos a un DCL. |
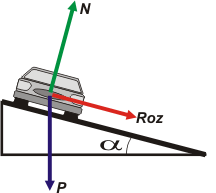 |
Supongamos que el coeficiente de rozamiento estático, μe, es un valor estándar y conocido para el par pavimento-caucho dibujado. En ese caso podríamos preguntarnos cuál debería ser el ángulo de inclinación para una velocidad máxima v en una curva de radio R.
En este problema pasa lo mismo que en el de peralte sin rozamiento, los estudiantes tienden a plantear las ecuaciones con un SR inadecuado, y aunque no es imposible resolver el problema se meten en un beregenal del que no es fácil salir airoso. |
|
|
|
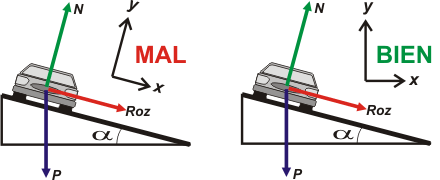 |
|
No es que esté MAL... es que es mucho más amigable el SR que te indico como BIEN.
También vas a encontrar en No me salen una resolución con el otro SR. |
|
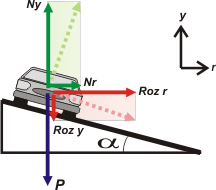 |
A ver si nos ponemos de acuerdo con el valor de las componentes.
Rozr = Roz cos α
Rozy = Roz sen α
Nr = N sen α
Ny = N cos α
¿Estamos de acuerdo? Entonces vamos a Newton. |
|
|
|
| Eje y |
→ ΣFy = m ay → |
Ny — P — Rozy = 0 |
[1] |
| Eje r |
→ ΣFr = m ac → |
Rozr + Nr = m ac |
[2] |
| Si se pretende velocidad máxima se corresponderá con el rozamiento estático máximo. Agreguemos una tercera ecuación. |
| |
RozeM = μe . N |
[3] |
| Y no nos olvidemos de que la aceleración centrípeta es: |
| |
ac = v2 / R |
|
[4] |
|
|
|
A partir de acá es todo álgebra. La física del problema se suspende por un rato. Entonces metemos todo en la licuadora... despejo Ny de la [1] reemplazando las componentes por sus iguales
N cos α = P + Roz sen α
otro tanto hago con la [2]
Roz cos α + N sen α= m ac
En estas dos ecuaciones que quedaron reemplazo la [3] y la [4]
N cos α = P + μe . N sen α
μe . N cos α + N sen α = m v2 / R
de ambas despejo N y las igualo
N ( cos α — μe sen α ) = m g
N ( μe . cos α + sen α ) = m v2 / R
Ahora divido miembro a miembro la segunda sobre la primera |
|
|
| |
|
μe . cos α + sen α |
= |
v2 |
|
|
|
| cos α — μe sen α |
R g |
|
|
|
Fijate que la expresión que obtuvimos sólo contiene nuestra incógnita, α, y el resto son los datos del problema: v, μe, R. Lo que sigue es un poco y engorroso y seguramente hay algun camino más corto y una forma de expresar el resultado más claro. Si querés probá vos por otro camino. Si querés segí mis pasos (los hice de a uno), si querés saltá directo a la discusión. Como quieras.
( μe . cos α + sen α) R g = ( cos α — μe sen α ) v2
R g μe . cos α + R g sen α = v² cos α — v² μe sen α
R g sen α + v² μe sen α = v² cos α — R g μe . cos α
sen α (R g + v2 μe) = cos α (v² — R g μe )
|
|
|
| tg α = |
|
v² — R g μe |
|
|
| R g + v2 μe |
|
|
|
| Divido numerador y denominador por Rg, y llegamos a |
|
|
|
|
|
DISCUSION: Ok, llegamos, te puede parecer complicado, pero no lo es, fijate. Las unidades dan, porque v²/R g no tiene unidades. μe tambiés es sólo un número, de modo que todo eso es nada más que una relación numérica, igual que una tangente. Por otro lado miremos qué pasa en situaciones extremas. Supongamos que no contamos con el rozamiento, hagamos μe= 0... queda que tg α = v²/R g que no es otra cosa que el resultado que obtuvimos en el problema 1.49.
Si α fuera 0º, en cambio, estaríamos en la situación del problema 2.10. No habría peralte y tendríamos que girar sólo con el rozamiento. En ese caso tg 0º = 0 implica que (v²/R g) — μe = 0 o sea μe = v²/R g que es el resultado que ya teníamos en ese caso. Todo cierra.
Pongamos un ejemplo numérico. Los ingenieros siempre tienen que pensar en las situaciones más desfavorables. El que maneja es un loco de esos que nunca faltan que va a 108 km/h (30 m/s), tenemos un día lluvioso de modo que el rozamiento es bajo μe = 0,4 y una curva cerrada R = 100 m. Hacemos las cuentas y nos da un ángulo α = 20º |
|
|
| DESAFIO: Un peralte de esa inclinación ya se hace peligroso para un automovilista prudente, lo cual pone a los ingenieros en un compromiso. ¿Cuál es ese compromiso y cuál es el límite máximo de un peralte? ¿Cómo calcularlo? |
|
| Algunos derechos reservados incluido el de llevar de paseo por una ruta sin peralte a quien me afane este material.
Se permite su reproducción citando la fuente. Agradezco la lectura atenta de Marco Vanotti que me envió una errata. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

