NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
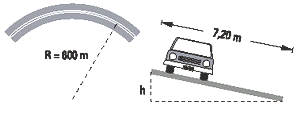
dN3.13b- La Ruta Nacional Nº 7 entre las localidades
de Chacabuco y Junín tiene un ancho de calzada
de 7,20 m. Para que un automóvil pueda circular
a 80 km/h por una curva de 600 m de radio
sin experimentar esfuerzos laterales, la diferencia
de nivel entre los bordes de la calzada debe
ser:
|
a) 0,082 m
b) 4,7 m
c)
0,82 m
d)
0,59 m
e) 1,06 m
f) falta la masa del automóvil. |
 |
|
|
|
BERENGENAL. Muchos estudiantes que se meten en el berengenal de intentar resolver el ejercicio del peralte con el sistema de coordenadas desaconsejable, inclinado. Vamos a recorrer esa curva peligrosa juntos. Odio las berengenas.
Las opciones se refieren a la altura h del esquemita. Un corte transversal de la ruta lo muestra como un triángulo rectángulo donde la hipotenusa es el ancho de la calzada. |
|
|
 |
De nuevo, voy a trabajar con el ángulo α en lugar de trabajar con h. La relación sigue siendo:
h = 7,20 m . sen α
|
|
|
|
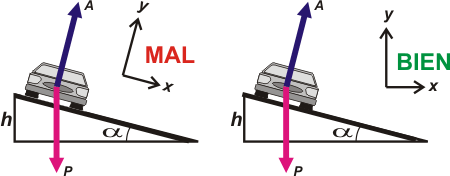
Te muestro los DCL y te recuerdo el asunto de los sistemas de referencia más usados: |
|
|
 |
|
|
Eran sólo dos fuerzas: la que hace la Tierra atrayendo al auto, su peso, , P; y la que hace el asfalto, A (por apoyo, que seguramente vos llamaste normal... no te preocupes, es la misma).
Pero como vos pertenecés al 83,56 % de los mortales que eligió el SR incorrecto y se metió en un berengenal... trataremos de salir juntos.
La clave de todo el asunto esta en la dirección de la aceleración. Reconozco que el sistema puede confundir un poco... y esconder la realidad del movimiento circular que estamos enfrentando. |
|
|
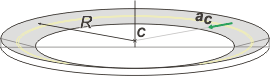 |
Este esquemita que tal vez te ayude a entender la dinámica de este MCU. La aceleración es de tipo centrípeta ¡y horizontal! |
|
|
|
 |
Tanto el radio de giro como el centro de la circunferencia como la aceleración centrípeta están al mismo nivel que el móvil, todo al ras del suelo... y no en un lugar bajo tierra.
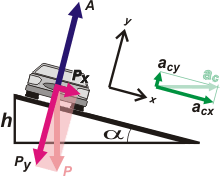
Con un sistema de referencia inclinado, no sólo tendremos que ocuparnos de descomponer alguna fuerza, también habrá que descomponer el vector aceleración.
Ahora sí, aplicamos ecuación de Newton para los dos ejes: |
|
|
|
eje y (que ya no es vertical) → ΣFy = m ay = m aCy
A — Py = m aCy
eje x (que ya no es horizontal) → ΣFx = m ax = m aCx
Px = m aCx
El ángulo formado entre aC y aCx... es α, nuevamente. También entre P y Py.
aCx = aC cos α, aCy = aC sen α
Px = P sen α, Py = P cos α
si meto estas igualdades en las ecuaciones de y y x...
A — P cos α = m aC sen α
P sen α = m aC cos α
A la primera ecuación la vamos a hacer esperar un poco porque la quiero usar para mostrarte algo interesante. En cambio, de la segunda podemos despejar α...
m g sen α = m aC cos α
Cancelando la masa y recordando que la aceleración centrípeta es v² / R... |
|
|
|
| |
Llegamos al mismo resultado que con el otro sistema de referencia.
Ahora mirá qué interesante lo que aparece si despejás de la primera ecuación la fuerza normal que realiza el pavimento, y reemplazás la aceleración centrípeta usando el resultado que acabamos de obtener:
A = P cos α + m aC sen α
|
|
|
| A = |
|
P cos α + m g sen² α |
|
|
| cos α |
|
|
|
| Masa por gravidad es iguala peso. |
|
|
| A = P ( cos α |
+ |
sen² α |
) |
|
| cos α |
|
|
|
Resolvé el paréntesis (suma de fracciones) y recordá la relación pitagórica:
cos² α + sen² α = 1
|
|
|
|
|
|
DISCUSION: Primero: este ejercicio nos dice -una vez más- que siempre tenés que ser capaz de arribar al mismo resultado independientemente del sistema de referencia que hayas elegido arbitriamente (ya vas a perder esa libertad cuando te dediques a la relatividad). Segundo: como ves en el último resultado la fuerza normal del pavimento es superior al peso (que está dividido por un número menor que uno)... contrariamente a lo que ocurre, por ejemplo, en un plano inclinado sin aceleración centrípeta (que podés encontrar en el ejercicio 1.10):
A = P . cos α
Los ingenieros de caminos inventaron el peralte, o sea, inclinaron el piso, para que sea el mismo piso el que haga doblar a los vehículos. Aprovechando la velocidad con la que ya llegan los autos a la curva, e inclinándola un poco, se consigue que la fuerza de apoyo provea una fuerza centrípeta autosuficiente o al menos adicional a la que habitualmente hace el agarre de los neumáticos. Meditalo. |
|
|
| DESAFIO: Elegí un tercer SR y resolvelo. |
|
 |
| Algunos derechos reservados.
Se prohibe terminantemente hacer uso de este material sin antes haber intentado resolver en problema en un grupo de estudio aplicado, mixto y en lo posible erótico. Se permite su reproducción citando la fuente. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
|

