NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Rozamiento)
|
|

|
NMS dN3.21- Determinar cuál debe ser la resultante de
las fuerzas aplicadas sobre un objeto de 1.000 kg que marcha a 72 km/h, para que describa una circunferencia
de 200 m de radio.
Si el objeto es un automóvil en una ruta horizontal,
calcular el mínimo coeficiente de rozamiento
(¿cuál?) entre sus neumáticos y el piso,
para que pueda mantenerse en la curva.
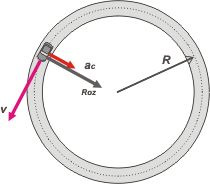
¿Te suena conocido este problema? Creo que ya lo hicimos... a ver... por qué no vas y te fijás el problema de cinemática 6.4. Es casi idéntico, el auto va a la misma velocidad, cambia un poquito el radio de la curva... pero poco. Te repito el esquema. |
|
|
|
Lógicamente, esa aceleración centrípeta es producto de una sumatoria de fuerzas. En este caso la única fuerza que apunta hacia el centro, la única fuerza que está haciendo doblar al auto y que lo mantiene sobre la curva es la fuerza de rozamiento. Supongo que nunca habrás probado girar sobre una mancha de aceite (lo más probable es que no estuvieras leyendo ésto...) pero lo podés imaginar.
Hagamos el DCL. |
|
|
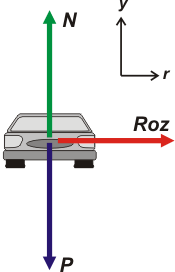 |
Bueno, ahí tenés. Un ejemplo más de que la fuerza de rozamiento no es opuesta a la velocidad. En este caso es perpendicular a ella, y le permite girar al auto hacia su izquierda (tu derecha).
Fijate también, en este caso, que se trata de un rozamiento estático. Que el auto se está moviendo no indica nada para este asunto. Estático o dinámico alude al problema de si hay o no hay deslizamiento entre las superficies. Y a menos que el auto patine, sus cubiertas no deslizan, se van apoyando mientras giran, y si tienen un buen agarre, no tienen por qué deslizar.
Bueno, vamos a las ecuaciones de Newton. Los ejes los llamé: y al vertical y r al radial. |
|
|
|
Eje y → Σ Fy = m ay → N — P = 0
Eje r → Σ Fr = m ac → Roz = m ac
Si se pretende el mínimo coeficiente de rozamiento (estático) éste deberá garantizar la fuerza para esta aceleración centrípeta, y será el coeficiente de rozamiento estático. Agreguemos una tercera ecuación.
RozeM = μe . N
Y no nos olvidemos que la aceleración centrípeta es
ac = v2 / R
Ahora metemos todo en la licuadora...
μe = RozeM / N
μe = m . ac / P
μe = m . ac / m . g
μe= ac / g
|
|
|
|
|
|
|
|
|
| La resultante no es otra que el rozamiento. |
|
|
|
|
|
| |
|
 |
| DESAFIO: El resultado genérico (recuadro amarillito) lo dice todo. Si el auto quiere ir más rápido tiene que preocuparse de que el coeficiente de rozamiento estático sea mayor que el que calculamos acá. Generalmente lo es... pero a veces no alcanza y eso pone un límite a la velocidad en las curvas. Cuando ese límite no se respeta (en el 96,73 por ciento de los casos) lo autos se despistan. Los ingenieros de vialidad inventaron entonces el peralte. Si te olvidaste qué corno era eso andá a ver el problema d3.10 y volvé, porque lo que te voy a proponer ahora es que combinemos las dos cosas: el peralte y el rozamiento. |
|
| Algunos derechos reservados.
Se permite su reproducción confesando de dónde lo afanaste... sin pressing. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

