 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, peralte)
|
|

|
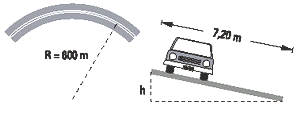
NMS d3.10- La Ruta Nacional Nº 7 entre las localidades
de Chacabuco y Junín tiene un ancho de calzada
de 7,20 m. Para que un automóvil pueda circular
a 80 km/h por una curva de 600 m de radio
sin experimentar esfuerzos laterales, la diferencia
de nivel entre los bordes de la calzada debe
ser:
|
a) 0,082 m
b) 4,7 m
c)
0,82 m
d)
0,59 m
e) 1,06 m
f) falta la masa del automóvil. |
 |
|
|
|
¿Te enojaste mucho con la resolución del problema 1.35? Bueno, mirá la figurita, eso es un peralte, una inclinación en la ruta que coincide con una curva y cuyo nivel inferior es el del lado interior de la curva. Lo construyen los ingenieros de caminos para facilitar la maniobra de doblar sobre la curva. Las curvas peraltadas se pueden tomar a mayor velocidad. Las curvas no peraltadas, o sea, horizontales, hay que tomarlas con menor velocidad porque siempre está el riesgo de salir despedido, o sea despistarse.
Parece obvio que todo buen conductor debe cerciorarse de que su vehículo tiene un buen "agarre" entre neumáticos y pavimento. No hay que salir a la ruta con las gomas "lisas", está claro que conducir bien depende en buena medida del rozamiento. Nadie intentaría doblar a 110 km/h sobre una mancha de aceite o sobre la escarcha o sobre ripio, porque sabe que se va hacia la banquina. Es la fuerza de rozamiento la que te permite doblar en las curvas, se trata de una fuerza que, en ese momento es lateral, y apunta hacia el centro de la curva. El peraltado ayuda a doblar, y hasta es capaz de hacerte doblar solito, sin necesidad del rozamiento.
La propuesta de este problema es justamente ésa: cuando te dice "sin experimentar esfuerzos laterales" está aludiendo a que no hay rozamiento, a que dobles solo por arte de peralte, si tenés ganas... en una pista enmantecada. Manos al volante, digo, a la obra.
Las opciones propuestas en el enunciado se refieren a la altura h del esquemita. Un corte transversal de la ruta lo muestra como un triángulo rectángulo donde la hipotenusa es el ancho de la calzada. |
|
|
 |
|
|
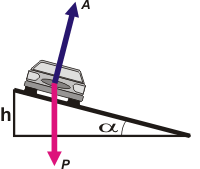
Por razones que te vas a dar cuenta más adelante yo prefiero trabajar con el ángulo α en lugar de trabajar con h. De todos modos es lo mismo, ya que están relacionados ambos con la hipotenusa:
h = 7,20 m . sen α
Como siempre, en dinámica, hay que arrancar por un DCL. |
|
|
 |
|
|
Si no hay rozamiento sólo actúan esas dos fuerzas. La que hace la Tierra atrayendo al auto, P, y la que hace el asfalto, A, apoyo, que (te aclaro, para que no desesperes) es perpendicular, o normal, al pavimento.
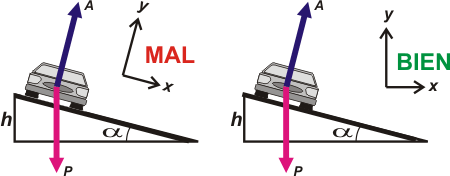
Como no son co-direccionales hay que descomponer al menos una de las fuerzas. Acá es donde casi todo el mundo mete la pata. No es que esté mal usar cualquier SR, sino que hay algunos más sencillos que otros. Como siempre tratamos de elegir un eje en la dirección (y sentido) de la aceleración y el otro ortogonal (con aceleración cero). El 83,56 % de los mortales elige el SR incorrecto y se mete en un berenjenal del cual no es fácil salir (*). |
|
|
 |
|
|
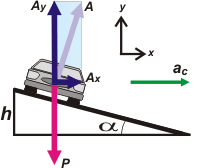
El movimiento del auto es circular, específicamente MRU, con v = cte = 80 km/h =
= 22,22 m/s. La aceleración, pues, es centrípeta... y ¡el centro de la circunferencia está a la misma altura del auto! La aceleración no apunta hacia abajo... es horizontal. En este último DCL la representé con un vector verde. |
|
|
 |
|
|
Ahora sí, aplicamos ecuación de Newton para los dos ejes:
eje vertical → ΣFy = m ay = 0
Ay — P = 0
eje centrípeto → ΣFx = m ax = m aC
Ax = m ac = m v²/ R
Ya casi llegamos. Fijate el ángulo formado entre A y Ay... ¡correcto! ¡es α! Lo cual implica que...
Ax = A sen α
Ay = A cos α
si meto estas dos cosas en las ecuaciones de x e y...
A sen α = m v²/ R
A cos α = m g
ahora divido miembro a miembro estas dos últimas ecuaciones, mirá lo que queda: |
|
|
|
| |
Esto que acabo de recuadrar no es la respuesta a este problema en particular, pero es la que vamos a discutir luego ya que constituye una descripción más general de los peraltes. Antes, terminemos el ejercicio.
|
|
|
| tg α = |
|
(22,22 m/s)² |
= 0,0823 |
|
| 600 m 10 m/s² |
|
|
|
α = arc tg 0,0823 = 4,70º
h = 7,20 m . sen 4,70º
|
|
|
| |
d) h = 0,59 m |
la respuesta correcta |
|
|
|
DISCUSION: No me digas que el autito de mis esquemas no es más modernoso que el de la guía, ¿viste? OK, ahora discutamos en serio la física del peralte. Fijate, sin rozamiento el auto igual dobla, logra la aceleración centrípeta requerida para doblar. La expresión de la inclinacion del peralte (sin rozamiento) es la que te recuadré en verde. No habla estrictamente de α, pero habla de la tg α. ¿Te acordás la función tangente? Si crece α también crece la tg α. Cuando α vale 0º, tg α también; y cuando α vale 90º, tg α creció infinito. Miremos qué dice nuestro resultado.
Las unidades son las correctas. A mayor velocidad (directamente proporcional su cuadrado a la tg α) mayor debe ser α. Sumamente lógico. Si la velocidad fuera cero no se nececesitaría peralte (ni curva). A mayor radio (es inversamente proporcional) menor inclinación de peralte. Lógico, mayor radio significa curva más suave, luego, no hace falta tanta fuerza para doblar. ¿Cuándo sería necesario un peralte inclinado 90º?
Todo cierra, esta discusión física no sólo es fácil y aleccionadora, me indica que llegué al resultado correcto mucho más eficientemente que revisando todo el planteo y el desarrollo algebraico 241 veces y media. La dinámica tiene un potencial intuitivo muy grande, hay que aprovecharlo. |
|
|
| *Si vos sos de los que intentó la resolución con el sistema de referencia inclinado y no pudiste salir del berenjenal... no desistas. Y si necesitás ayuda la vas a encontrar aquí. |
|
|
| DESAFIO: ¿Puede un automovilista girar en un curva peraltada sin volantear? |
|
 |
| Algunos derechos reservados.
Se prohibe terminantemente hacer uso de este material sin antes haber intentado resolver en problema en un grupo de estudio aplicado, mixto y en lo posible erótico. Se permite su reproducción citando la fuente. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

