 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme) |
|

|
 |
NMS c2.04 - Juan, cronómetro en mano y ubicado en un tramo rectilíneo de una ruta, estudia el movimiento de los coches que circulan por la misma con velocidad constante. A su derecha, y a 40 metros de él hay un árbol, y más lejos un cartel. En cierto instante ve que un automóvil se le acerca por la izquierda y dispara el cronómetro cuando lo tiene a 100 metros; el auto pasa frente a él 5 segundos después. Utilizando como origen la posición de Juan y los tiempos que indica el cronómetro: |
a - Hallar el vector velocidad del auto, y la indicación de su velocímetro en km/h. Escribir su ecuación horaria.
b - Hallar en qué instante pasará el auto frente al árbol.
c - Si cuando el cronómetro indica 10 segundos el auto pasa frente al cartel, cuántos metros hay entre éste y el árbol.
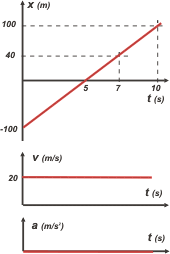
d - Hacer los gráficos x(t) y v(t), indicando el paso del auto frente al árbol y al cartel.
e - Con el mismo origen y sentido positivo, hacer los gráficos para otro auto que se mueve en sentido contrario con la misma rapidez, acotando los tiempos que indicará el cronómetro, hasta que llegue a 100 m a la izquierda de Juan. (Elegir en qué instante se pone en marcha el cronómetro). |
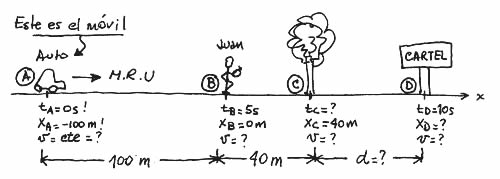
Bueno, bueno, que no cunda el pánico. Siempre se empieza por un esquema. Esto tiene muchas utilidades pero... ¿cómo se hace? Fácil: a) se dibuja la trayectoria, b) se indican los puntos notables, aquellos de los que habla el enunciado, c) se les pone nombre, d) se indican (al lado de cada punto) las características cinemáticas t, x, v, con su nombre correspondiente, e) se ponen los valores a cada constante indicada. En este caso queda algo así:
|
| |
 |
|
Así eran los esquemas de No me salen cuando lo editaba en papel. |
| Nota: de todas la herramientas para hacer cinemática el esquema es la de más fácil implementación, fácil interpretación, permite dar una idea global del problema, una ordenación espacio-temporal de los eventos que ocurren. Es la mejor forma de organizar los datos de un problema y establecer el sistema de referencia (SR). Nos obliga a algo fundamental: ponerle nombre a todas las cosas de las que podemos llegar a hablar durante la resolución del problema. Y lo más importante: es la mejor oportunidad (hacer un esquema) de CONTRASTAR nuestra interpretación de los hechos con lo que verdaderamente dice el enunciado. |
|
|
|
Ahora escribimos la ecuación horaria del móvil. Nos remitimos al modelo de ecuación correspondiente, en este caso, el modelo del MRU:
x = xo + v ( t – to )
En él reemplazamos las constantes (to, xo y v) por las constantes "iniciales" de nuestro problema, por ejemplo las del punto A. OJO: para armar la ecuación horaria NO TOCAR NI REEMPLAZAR LAS VARIABLES DE LA ECUACION (t y x). Entonces queda así:
x = – 100 m + v . t
Ahora el problema no tiene más secretos para nosotros. Todo lo que quieras se le puede preguntar a esa ecuación. Fijate que esa ecuación "habla" de todos los infinitos puntos por los que pasa el automóvil y sus respectivos instantes de tiempo. Bien, basta con que le pidamos que "hable" en particular de aquellos puntos que para nosotros tienen interés, o sea, el B, el C y el D. Todavía no sabemos cuánto vale v... no te hagas problema, vos usala igual, confiá en la ecuación horaria.
Si habla del B (mirá el esquema) dirá:
0 m = – 100 m + v . 5 s [1]
Viste que lo que hice fue reemplazar x y t, las variables. Donde decía x, puse xB y donde decía t puse tB. Lo demás no lo toqué. Ahora hago lo mismo para todos los otros puntos que me interesen. Si habla del C (mirá el esquema) dice:
40 m = – 100 m + v . tC [2]
Si habla del D (mirá el esquema) dice:
xD = – 100 m + v . 10 s [3]
Tenés 3 ecuaciones y 3 incógnitas. O sea, ya está resuelto. Lo que queda es álgebra, no física. Igual te lo hago para que no llores. De la [1] despejo y calculo v.
v = 100 m / 5 s
v = 20 m/s, o, si querés,
|
|
|
|
|
|
Con el valor de v, voy a la [2], despejo y calculo tC. |
|
|
| tC = |
|
( 40 m + 100 m ) |
|
|
| 20 m/s |
|
|
|
|
|
|
Y también voy a la [3], saco xD:
xD = 100 m, entonces, d = 100 m – 40 m
|
|
|
|
|
|
|
|
|
| |
 |
Como ves, todos los ejercicios de cinemática se resuelven de la misma manera. No hace falta "encontrarles la vuelta". Es un asunto mecánico, automático.
Los gráficos los hago en forma encolumnada y con una misma escala de tiempo. Esta disposición tiene algunas ventajas muy interesantes. Ahora no las podés apreciar, pero más adelante, cuando seas grande, vas a ver qué interesantes son.
El orden en que los encolumno tampoco es arbitrario, tiene que ver con la teoría de funciones y derivadas. Es un orden lógico y natural. ¡La pucha!
Cuando seas grande... vas a ser grande. Yo también, no te creas... |
|
|
|
| DESAFIO: Cuando armamos la ecuación horaria elegimos el punto A como "inicial" para reemplazar las constantes (to , xo , y v). Elijamos ahora el punto B y volvamos a resolver el problema. |
|
|
| |
|
|
| Nota: Me embola escribir m/s (metro sobre segundo) de esa forma, con la raya oblicua. Lo correcto es escribir la m justo arriba de la s y la raya horizontal. Pero todavía no se puede editar eso en html (me refiero a: sin tener que insertar una imagen). (Más información sobre esta cuestión aquí). |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severas. Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
| |
|

