 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
| |
 |
FIS c5.02 - Un gato maúlla con ganas, instalado sobre un muro de 2 m de altura. Juan está en su jardín, frente a él y a 18 m del muro, y pretende ahuyentarlo arrojándole un zapato. El proyectil parte con una velocidad de 15 m/s, formando 53° con la horizontal, desde una altura de 1,25 m.
a - Hallar a qué altura por encima del gato pasó el zapato.
b - Determinar a qué distancia del otro lado del muro llegó el zapato al piso. |
|
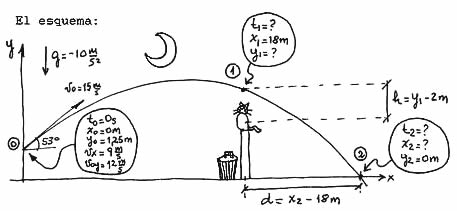
| En los ejercicios de Tiro Oblicuo, más que nunca, hay que empezar por un esquema. Este de aquí me quedó de cuando hacía los No Me Salen a mano. Qué loco, ¿no? |
 |
|
|
Por qué puse el origen de referencia en el piso, bueno, porque algunos datos que da el enunciado ya vienen referidos al piso: "un muro de 2 m de altura", etc. Me resulta más fácil pensar las cosas así. Pero cualquier otro sistema de referencia hubiera servido igual. ¿Cuántas ecuaciones horarias describen este problema? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
vx y voy no son datos del enunciado. En cambio nos dan la velocidad real, vo , con la que sale disparado el zapato y el ángulo de disparo. Bien, con eso alcanza...
vx = vo cos 53° = 15 m/s . 0,6 = 9 m/s
voy = vo sen 53° = 15 m/s . 0,8 = 12 m/s
Esos son los valores que puse en el esquema, en el globito que habla del punto 0. Con todas esas constantes, entonces, armamos las ecuaciones que describen el movimiento del zapato. | |
|
| |
x = 9 m/s . t
y = 1,25 m + 12 m/s . t – 5 m/s² . t²
vy = 12 m/s – 10 m/s² . t
|
|
| Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado. |
|
| Lo que resta ahora es muy sencillo; basta con que les pidamos a las ecuaciones del zapato que hablen de los puntos de interés en el problema: el 1 y el 2. Pero a la ecuación de velocidad vertical le vamos a dar descanso: ningún dato aportan sobre velocidad los puntos 1 ni 2. Ni tampoco nos preguntan nada sobre velocidad en esos puntos. Veamos. |
|
|
 |
18 m = 9 m/s . t1 |
|
[1] |
| y1 = 1,25 m + 12 m/s . t1 – 5 m/s² . t1² |
|
[2] |
| x2 = 9 m/s . t2 |
|
[3] |
| 0 m = 1,25 m + 12 m/s . t2 – 5 m/s² . t22 |
|
[4] |
|
|
| Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
|
Me lo temía: quedó un sistema de tantas ecuaciones como incógnitas (4x4), en las que las incógnitas, si sabemos interpretarlas, son las que nos pide el enunciado del problema. Quiere decir que acá terminó la física del problema... lo que resta es álgebra. Y es bastante sencilla. Si lo mirás con cariño te das cuenta de que las dos primeras forman un sistema chiquito (2x2) y las dos últimas, otro. Se resuelven por separado. Fijate: |
|
|
De la ecuación [1] despejás t1; alcanza con que pases dividiendo los 9 m/s al primer miembro. Te queda t1 = 2 s. Ese es el instante en el que el zapato pasa justo por arriba del gato (o lo estampa, todavía no sabemos). Andá haciéndolo conmigo, no seas vago.
Ahora ese resultado, t1 = 2 s, lo metemos en la ecuación [2]. Volvé a escribirla, pero cada vez que dice t1, escribí 2 s. Tené cuidado, mirá que (2 s)² = 4 s². Después de reemplazar, multiplicás, sumás, restás y obtenés y1 que te da: y1 = 5,25 m.
Pero el enunciado preguntaba cuánto por encima del gato pasó el zapato, y el gato estaba a 2 m. Llamemos h a la altura que buscamos, entonces
h = 5,25 m – 2 m
|
|
|
|
|
|
Ahora vamos a trabajar con las otras dos ecuaciones, la [3] y la [4]. Siempre hay que empezar con la ecuación que tiene menos incógnitas, en este caso la [4], cuya única incógnita es t2, el instante en que el zapato toca el piso. Hay un problema: no se puede despejar así nomás (si no me creés probá) porque aparece una vez elevada al cuadrado, pero no te preocupes... los griegos inventaron una formulita que resuelve el problema y que hay que tener siempre a mano: |
|
|
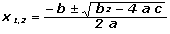
|
|
|
x1.2 representa la variable que sea, en nuestra ecuación es t2, pero como en toda cuadrática vamos a tener dos resultados, uno es el que buscamos, el otro es un colado. Para usar la formulita de los griegos hay que tener cuidado de que la ecuación esté igualada a cero. Por suerte es nuestro caso: c es el término independiente, b es el coeficiente lineal y a el coeficiente cuadrático. Te los paso en limpio:
c = 1,25 m, b = 12 m/s, a = – 5 m/s²
|
|
|
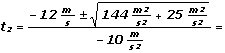
|
|
|
Usando una vez el "+" y otra vez el "-", encontramos los dos valores de t2 que nos dan:
t2 = 2,5 s y t2´= – 0,1 s
No cabe duda de cuál es el bueno y cuál el colado. Ahora metemos ese resultado en la ecuación [3] y resulta
x2 = 9 m/s . 2,5 s = 22,5 m
Entonces la distancia desde el muro es
d = 22,5 m – 18 m
|
|

| Obvio... no vas a tirar un zapato nuevo. |
|
|
|
|
| A buscar el zapato del otro lado. ¿Te diste cuenta de que sólo recuadro las respuestas al enunciado? |
|
DESAFIO: El gato no vio salir el zapato por la ventana y por lo tanto no sabe desde qué altura salió. Es más, él cree que el zapato es un objeto volador de tiros oblicuos que salió lanzado desde el piso. Sin hacer operaciones que no sea mentalmente, decir cuánto debe suponer el gato que duró el vuelo del zapato. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. También se permite que sea sin reproducción... ¿se comprende? Última actualización ago-06. Buenos Aires, Argentina. |
|
|
| |
|

