|
NO ME SALEN
SOLVED PROBLEMS IN PHYSICS
(Projectile Motion)
|
|

|
 |
5.4 - A cat meows, installed on a 2m height wall. Juan is in his garden, in front of him and at 18 m from the wall, and he pretends to drive him away by throwing a shoe. The projectile starts out with 15 m/s speed, forming 53° to the horizontal, from a 1,25m height.
a - Determine how high above the cat passed the shoe.
b - Determine how far, in the other side of the wall, the shoe reached the floor. . |
|
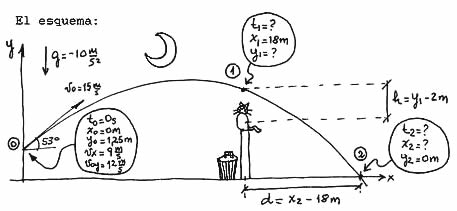
| In oblique shot exercises, more than ever, we must begin with a diagram. I've got this one here, when I used to do the exercises by hand. Crazy, right? |
 |
|
|
Why did I put the reference origin on the floor?, well, because some data (that the statement gives) are already referred to the floor: "a 2 m height wall", etc. I find it easier to think things that way. But any other reference system would have worked equally. How many time equations describe this problem? Three, of course, like every OS. To find them you have to simply replace the constants (to , xo , yo , vx , voy , and g) of the oblique shot´s general equations:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy+ g ( t – to )
vx and voy are not set out data. Instead we get the actual speed, Vo, with which the shoe goes away, and the firing angle. Good, that's enough...
vx = vo cos 53° = 15 m/s . 0,6 = 9 m/s
voy = vo sen 53° = 15 m/s . 0,8 = 12 m/s
Those are the values I put in the scheme, in the ballon that is talking about the 0 point. With all those constants, then, we setup the equations that describe the motion of the shoe. | |
|
| |
x = 9 m/s . t1
y = 1,25 m + 12 m/s . t – 5 m/s² . t²
vy = 12 m/s – 10 m/s² . t
|
|
| Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado. |
|
| What´s left is very simple now; it is enough with asking to the shoe´s equations to talk about the interest points of the problem: the 1 and the 2. But we will give a rest to the vertical speed equation: no data is provided about speed in the first and second point. Nor they ask us anything about speed in these points. Let´s see. |
|
|
 |
18 m = 9 m/s . t1 |
|
[1] |
| y1 = 1,25 m + 12 m/s . t1 – 5 m/s² . t1² |
|
[2] |
| x2 = 9 m/s . t2 |
|
[3] |
| 0 m = 1,25 m + 12 m/s . t2 – 5 m/s² . t22 |
|
[4] |
|
|
| Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
|
I feared this: it was a system of many equations as unknowns (4x4), in which the unknowns, if we know to interpret them, are the ones that the problem´s statement asks. It means that here finished the physics of the problem... the rest is algebra. And it is quite simple. If you you look fondly you realize that the first two are a little system (2x2) and the last two, another. They are solved separately. Look: |
|
|
From the equation [1] you clear t1; it is enough if you pass 9 m/s dividing the first term. You have left t1 = 2 s. That is the instant in which the shoe goes right above the cat (or hits him, we still don´t know). Start doing it with me, don´t be a bum.
Now this result, t1 = 2 s, we put it into the equation [2]. Write it again, but every time it says t1, you write 2 s. Be careful, because (2 s)² = 4 s². After replacing, you multiply, addition, subtraction and you get y1 which gives: y1 = 5,25 m.
But the statement was asking how much above the cat, the shoe passed, and the cat was 2 m high. Let´s call h to the height we are looking for, so
h = 5,25 m – 2 m
|
|
|
|
|
|
Now we are going to work with the other two equations, the [3] and the [4]. Always start with the equation that has fewer unknowns, in this case the [4], whose only unknown is t2, the instant in which the shoe touches the floor. There is a problem: it can't be clear just like that, but don´t worry... the greeks invented a tiny formula that solves the problem and that you need to have always with you:
|
|
|
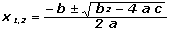
|
|
|
x1.2 represents any variable, in our equation is t2, but as in any quadratic we will have two results, one of them is the one we are looking for, and the other one is useless. To use the greeks´s formula beware that the equation is equal to zero. Fortunately in our case: c is the constant term, b is the linear coefficient, and a is the quadratic coefficient:
c = 1,25 m, b = 12 m/s, a = – 5 m/s²
|
|
|
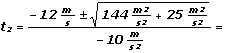
|
|
|
Using for once "+" and once again "-", we find the two values of t2 that gave us:
t2 = 2,5 s and t2´= – 0,1 s
No doubt, that one of them is good and the other is not. Now we put this result in the equation [3] and turns out
x2 = 9 m/s . 2,5 s = 22,5 m
Then, the distance from the wall is
d = 22,5 m – 18 m
|
|

| Obvio... no vas a tirar un zapato nuevo. |
|
|
|
|
| To find the shoe on the other side. Did you notice that I only box the answers to the questions? |
|
CHALLENGE: The cat didn´t see the shoe coming out the window and, therefore, he do not know from what height left. Moreover, he thinks that the shoe is a flying object of oblique shots fired from the floor. Without operations than mentally, say how much should the cat assume that lasted the flight of the shoe. |
|
 |
| Translated by Florencia Torres . Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last Updated March-14. Buenos Aires, Argentina. |
|
|
|
| |
|