8.1 - Para el tiro oblicuo planteado en el problema 5.2, determinar el radio de curvatura de la trayectoria, y las componentes tangencial y normal de la aceleración del perdigón, en el punto más alto de su trayectoria, y en el instante t = 6 segundos.

Para resolver este problema tenés tres condiciones: a) haber resuelto íntegramente el problema 5.2, y tres o cuatro más de tiro oblicuo; b) haber estudiado movimiento circular y haber resuelto unos cuantos problemas de la guía correspondiente; y c) haber leído el artículo de complemento teórico de cinemática escalar.

Si reunís las tres condiciones... adelante. Vamos a observar atentamente las dos posiciones en que nos piden hallar el radio de curvatura; te lo voy a mostrar ampliado y por separado. El segundo punto ofrece más dificultades que el primero. Si recordás el problema 5.2, los llamé M y N.

M = P_(3s) = 120 m î ; 45 m ĵ

v_M = 40 m/s î + 0 m/s ĵ

|v_M| = 40 m/s

Para hallar el radio de curvatura en M usaremos

R_M = v_M² / a_cM

a_cM no es otra que la aceleración de la gravedad, igual a 10 m/s², aproximadamente, que es la única aceleración durante todo el movimiento y que es constante en módulo, dirección y sentido. En el punto M, y sólo ahí, es, además, perpendicular a la velocidad, y por lo tanto centrípeta. De modo que

R_M = v_M² / g

Ahora hallemos el radio de curvatura en N. Es un poco más difícil, pero no arrugues. Si te acordás, el punto N, que lo llamé así por "nivel", se alcanzaba a los 6 segundos, y la altura del proyectil volvía a ser cero. El ángulo que formaba la velocidad con la horizontal volvía a ser el mismo que el de partida, pero hacia abajo; en nuestro caso α valía 37 grados.

N = P_(6s) = 240 m î ; 0 m ĵ

v_N = 40 m/s î — 30 m/s ĵ

|v_N| = 50 m/s

Acá tenés un gráfico; disfrutalo, que me costó bastante hacerlo.

Para hallar el radio de curvatura en N usaremos

R_N = v_N² / a_cN

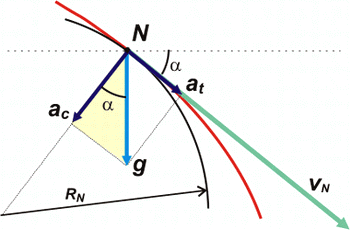
El nuevo problema que se nos presenta es, justamente, hallar a_cN , la aceleración centrípeta en N. Para eso hay que descomponer la aceleración real, g, en dos direcciones: una tangencial (que no nos importa mucho) y otra centrípeta (que es la que nos interesa). La dirección de la tangente no es otra que la dirección de la velocidad y en nuestro caso vale 37 grados. Y si no supiéramos cuánto vale α haríamos α = arc tg v_y / v_x (ya lo hiciste 30 mil veces). Pero ahora sabemos que vale 37 grados. Para hacer la descomposición conviene hacer un esquemita y no perderse.

Tú lo has dicho: a_cN = g . cos α, entonces nos queda

R_N = v_N² / g cos α

DISCUSION: Este análisis del radio de curvatura es tremendamente descriptivo. Si mirás el último esquemita que hice verás que representé, además de la aceleración centrípeta, la aceleración tangencial (superpuesta a la velocidad, necesariamente). Esa componente, a_t , que es igual a g . sen α, es la que describe la variación del módulo de la velocidad del móvil: si va más rápido o más lento. Vos sabés que cuando el móvil animado de un tiro oblicuo va en bajada, el ángulo que forma con la horizontal, α, va en aumento; por lo tanto es lógico que cada vez vaya más rápido y que cada vez doble menos, es decir, que vaya más derecho.

Tangente viene del griego y quiere decir tocante. La aceleración tangencial es la común y silvestre que viste desde principios de MRUV. Tiene la misma dirección que la velocidad y que la trayectoria en cada posición, de ahí viene el nombre.

Hay quien sube un SR portátil al móvil, con lo cual se desentiende de los cambios de dirección. A esa pirueta la llaman coordenadas intrínsecas, la aceleración centrípeta desaparece y el tratamiento cinemático vuelve a ser igual que en los movimientos rectilíneos. Por eso a este capítulo le pusieron "cinemática escalar"; son juegos.

La tangente (la recta que toca) y el círculo osculatriz (la circunferencia que besa) son herramientas de gran utilidad. La primera nos aclara la dirección del movimiento, la segunda su curvatura. Parece ser que tocar y besar son tan imprescindibles en la física como en la vida.

DESAFIO: Si vos fueras ingeniero de caminos y tuvieses que diseñar una ruta, al planificar las curvas, las proyectarías como arcos de circunferencia o como arcos de parábola... y por qué. Si te doy a elegir entre esas dos variantes, una sola es la correcta; sin embargo, se prefieren las trazas mixtas. ¿Cómo son y por qué?

¿Te puedo recomendar un libro que te vas a devorar?