NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
 |
FIS c5.05.2- Se dispara un perdigón con un rifle de aire
comprimido, desde lo alto de una colina. El
proyectil parte con una velocidad de 50 m/s, en
una dirección que forma un ángulo de 37°con la
horizontal. Elegir un sistema de referencia, y despreciando
todo rozamiento: |
|
|
a - Hallar la posición del perdigón a los 2 s, 5 s
y 8 s después de haber partido, respectivamente.
Representar en un diagrama x-y.
b - Determinar las componentes de los vectores
velocidad en los instantes anteriores. Representar
dichos vectores en las cuatro posiciones
conocidas del diagrama anterior.
c - Hallar en qué instante se encuentra al mismo
nivel que el de partida, qué posición ocupa y
cuál es su velocidad en ese instante.
d - Sin hacer cuentas, justifique entre qué instantes
de los especificados cree usted que el proyectil
alcanzará la máxima altura. ¿Qué velocidad
tendrá allí? Calcúlelo ahora y verifique su hipótesis.
e - Con toda la información anterior, dibujar la
trayectoria del proyectil. Escribir la ecuación de
la misma. |
|
| |
Ok, ok... no nos dejan hacer nada original. Vamos a armar las ecuaciones horarias sin hacer el esquema... espero no equivocarme. Los modelos son éstos:
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy + g ( t – to )
tomando to = 0, xo = 0 y yo = 0 (todo eso fue elección mía, arbitraria), y razonando que vx= v0 cos 37º = 40 m/s, y voy = v0 sen 37º = 30 m/s, nuestras ecuaciones quedan así:
|
|
|
x = 40 m/s . t
y = 30 m/s . t — 5 m/s² . t²
vy = 30 m/s — 10 m/s² . t
|
|
| estas son las ecuaciones que describen todo el movimiento del perdigón |
|
a) Ahora les pedimos a esas ecuaciones que hablen de tooooodos los puntos que al enunciado se le ocurran. Yo te muestro cómo obtengo el primer par, vos hacés solo el resto, ¿dale? Doy los resultados en forma de par ordenado (en metros) y además les pongo un nombre: A, B y C.
x(2s) = 40 m/s . 2 s
y(2s) = 30 m/s . 2 s — 5 m/s² . (2 s)²
|
|
|
| |
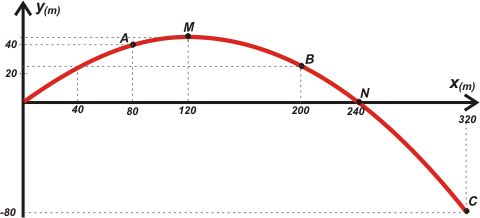
A = P(2s) = 80 m î ; 40 m ĵ |
|
| |
B = P(5s) = 200 m î ; 25 m ĵ |
|
| |
C = P(8s) = 320 m î ; —80 m ĵ |
|
|
|
|
| Ahora viene el gráfico x-y. Acá te lo hice. Fijate que aproveché y marqué dos puntos más, el M y el N, de los que se habla más adelante. No representé los vectores de velocidad porque el gráfico se ponía un poco complicado y chiquito. Imaginátelos o hacelo vos. Pero si tenés dudas podés ir al problema 7.1, en el que se vuelve a hablar de este mismo problema y, en especial, de sus velocidades. |
|
|
 |
|
|
b) Ahora vamos a calcular las velocidades. La componente horizontal de la velocidad se mantiene constante (como en todo tiro oblicuo) y vale 40 m/s. La componente vertical se la tenemos que pedir a la tercera ecuación del tiro. Te muestro cómo es para el punto A, vos lo hacés para los otros dos.
vy(2s) = 30 m/s — 10 m/s² . 2 s = 10 m/s
|
|
|
| |
vA = 40 m/s î + 10 m/s ĵ |
|
| |
vB = 40 m/s î — 20 m/s ĵ |
| |
vC = 40 m/s î — 50 m/s ĵ |
|
|
|
c) Para saber en qué instante se halla en el mismo nivel que en la partida le pido a la segunda ecuación que lo describa.
y = 30 m/s . t — 5 m/s² . t²
ella dice, entonces
0 m = 30 m/s . t(0m) — 5 m/s² . t(0m)²
despejo t(0m). Es fácil porque es cuadrática... pero incompleta. Así que saco factor común t(0m)
0 m = t(0m) . ( 30 m/s — 5 m/s² . t(0m) )
Y aparecen los dos instantes de tiempo en que la altura vale cero. El primero es obvio, cuando t(0m) = 0, el segundo es el que me interesa, cuando todo el paréntesis vale cero.
t(0m) = 6 s
con ese valor voy a la ecuación de x y de vy para hallar todo lo que me piden de ese punto al que llamé N (por nivel)
x(6s) = 40 m/s . 6 s
vy(6s) = 30 m/s — 10 m/s² . 6 s
|
|
|
| |
N = P(6s) = 240 m î ; 0 m ĵ |
|
| |
vN = 40 m/s î — 30 m/s ĵ |
|
|
|
|
d) Sin hacer cuentas y apelando a que toda parábola es simétrica: si está en el nivel cero en los x igual a 0 y 240 metros, se hallará en la altura máxima (punto al que llamé M) justo en la mitad, o sea en el x igual a 120 metros.
Hallarlo analíticamente no es difícil. En esa posición de máxima altura la velocidad vertical se anula. Le pido a la ecuación que describe las velocidades verticales que lo describa. Ella dice: |
|
|
0 m/s = 30 m/s — 10 m/s² . tM
despejo tM
tM = 30 m/s / 10 m/s²
tM = 3 s |
 |
|
|
|
| con esta información voy a las ecuaciones de posición x e y |
|
|
| |
M = P(3s) = 120 m î ; 45 m ĵ |
|
| |
vM = 40 m/s î + 0 m/s ĵ |
|
|
|
|
e) el gráfico de la trayectoria es justamente el que tenés arriba; se deben haber equivocado al redactar el problema porque, justamente, lo que están faltando son los gráficos de posición, velocidad y aceleración en función del tiempo. Hacelos vos... media pila, ¡dale!
En cuanto a la ecuación de la trayectoria, la idea consiste en fabricar una ecuación de y en función de x. Se procede así: de la ecuación de x despejamos la variable t
x = 40 m/s . t ⇒ t = x / 40 m/s
ahora, en la ecuación de y, reemplazamos t por la expresión que obtuvimos recién (guarda que tenés que reemplazarlo dos veces, y una de ellas elevándolo al cuadrado):
y = 30 m/s . t — 5 m/s² . t²
y = 30 m/s . (x / 40 m/s) — 5 m/s² . (x / 40 m/s)²
y = 0,75 x — 5 m/s² . (x² / 1600 m²/s²)
|
|
ayudame a mejorar el
CBC |
|
|
|
Si la mirás con cariño y sin mucho odio te das cuenta de que es una ecuación cuadrática, lo cual confirma que la trayectoria de un tiro oblicuo es una parábola parabólica aparabolicada desde el principio hasta el final. Fuera de joda: mirá que no es simétrica; la simetría sólo cuenta entre valores de igual y, o sea que el eje de simetría es una recta vertical que pasa por el x de altura máxima. Chau. |
|
 |
| DESAFIO: ¿A qué altura se halla el perdigón en el x = 205 m? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco la corrección que me envió Sabrina. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
| | | |
|

