NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
|
|

|
CINEMATICA ESCALAR
Breve explicación sobre los conceptos que aparecen en este capítulo: radio de curvatura, aceleración tangencial y otros
Radio de curvatura... ¿qué es eso?, ¿con qué se come? Ok, empecemos por ahí. Admitís que el móvil en el tiro oblicuo no se desplaza en línea recta, ¿de acuerdo? Bien, si no va en línea recta entonces va doblando. La curva que "dibuja" en el aire es una parábola; bien dicho sería: la trayectoria es un arco de parábola. Hasta aquí no hay ninguna novedad.
Suponete que vas en auto, manejando vos, y por una ruta en la llanura, todo horizontal. Pero la ruta tiene una curva que vista de arriba tiene forma de parábola. Cuando ingresás a la curva (por una de las ramas de la parábola) girás muy poco el volante. Pero a medida que seguís avanzando la curva se cierra más y más. En el vértice de la parábola el giro de tu volante (el torcimiento o desvío de las ruedas) fue máximo, y a partir de ahí las fuiste enderezando suavemente.
El radio de curvatura es el concepto que describe físicamente este relato (o uno semejante). Mirá este esquemita, después avanzamos. |
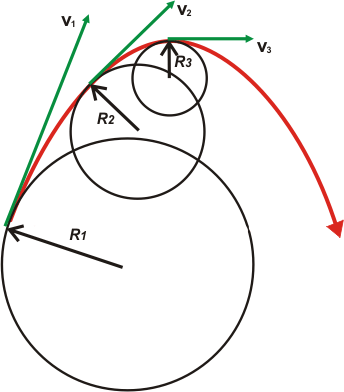
|
| En este gráfico te muestro, en rojo, la trayectoria parabólica de un tiro oblicuo. Fijate que las velocidades, en verde, siempre son tangentes a la trayectoria. En el mismo punto de tangencia podés apoyar una circunferencia osculatriz, que te indica cuán curvada es la trayectoria en ese lugar. |
|
Cuanto mayor es el giro, cuanto más girado tenés el volante, menor es el radio de curvatura... menor es la circunferencia hipotética que tiene una curvatura igual a la que estás girando en ese instante.
Por el contrario, cuanto menor –o más suave– es la curvatura de la ruta, mayor es el radio de giro, o sea, mayor es la circunferencia hipotética que tiene una curvatura igual a ésa en la que estás girando en ese momento.
A esa circunferencia hipotética se la llama circunferencia osculatriz (que si no me equivoco quiere decir algo así como "circunferencia que besa", ya que ósculo quiere decir beso). Voy a tratar de resumirlo: cuando un móvil está doblando, sea sobre la curva que sea, y sea sobre la trayectoria que sea, siempre se puede pensar que está doblando sobre una circunferencia que tiene igual curvatura que la trayectoria en ese momento. Bien. Esa circunferencia tiene un radio (como toda circunferencia); acá lo llamaremos radio de curvatura, y sirve para caracterizar a la curva en ese punto. ¿Te cerró?
Ahora vamos a ver cómo se calcula. La idea de la circunferencia es muy fecunda porque, entre otras cosas, nos remite a los movimientos circulares. La condición necesaria para estar en un movimiento circular es poseer una aceleración centrípeta (que asegura que la dirección de la velocidad cambie, o sea, que podamos doblar). Si mal no recuerdo la aceleración centrípeta es:
ac = v2 / R
esta expresión nos sirve para hallar el radio de la circunferencia osculatriz, o sea, independientemente de cuál sea la trayectoria en particular. |
|
Cuanto más chico es el radio de curvatura, más chica es la circunferencia osculatriz, más frecuentemente se escucha: "¡Loco, qué curva cerrada!" ¿Te cerró? |
| |
|
|
Para calcularlo debemos conocer la velocidad tangencial y la aceleración centrípeta.
DISCUSION: Tiene las unidades correctas: una velocidad al cuadrado, dividido por una aceleración, se mide en unidades de longitud... que es lo correcto para un radio. Si el radio fuera infinitamente largo indicaría que te estás moviendo sobre una recta (tu aceleración centrípeta tendría que ser cero o casi cero). Por el contrario, si quisieras pegar un giro abrupto (una curva angulosa) el radio de curvatura tendría que valer cero o casi cero.
La matemática no permite dividir por cero y el universo no permite doblar en forma angulosa. Así como para pasar de una velocidad de 20 km/h a otra de 40 km/h el universo te obliga a pasar por todas las velocidades intermedias, del mismo modo, para cambiar de una dirección a otra, estás también obligado a pasar por las infinitas direcciones intermedias. ¿Por qué será nuestro universo tan endiabladamente lógico? |
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
| | | |
|

