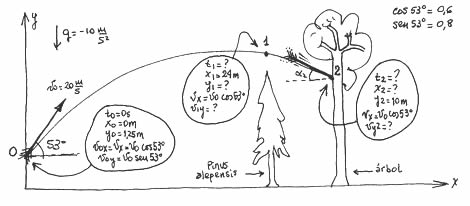
Como siempre, comenzamos con un esquema. Dibujamos la trayectoria, identificamos los puntos que presentan interés, les ponemos nombre, escribimos las características cinemáticas de cada punto, y ponemos los datos del problema eligiendo el SR.

Cualquier otro SR hubiera servido del mismo modo; elegí éste porque me pareció el más económico para responder las preguntas.

Vamos a armar las ecuaciones horarias que describen el movimiento de la flecha. Para ello hay que tener a mano los modelos de ecuación horaria (son los de TO), y en ellos reemplazar las constantes ( t_o , x_o , y_o , v_x , v_oy , y g) por las constantes iniciales del problema.

x = 12 m/s . t

y = 1,25 m + 16 m/s . t – 5 m/s² . t²

v_y = 16 m/s – 10 m/s² . t

Ahora las usamos, o sea, les pedimos a estas ecuaciones que hablen de los puntos de interés: el 1 y el 2; fijate, figuran en el esquema.

Y, como siempre, desembocamos en un sistema de tantas ecuaciones como incógnitas (5x5), bastante sencillo, en el que las incógnitas, si sabemos interpretarlas, son las que nos pide el enunciado del problema.

Fijate que no le pedimos a la ecuación de velocidad que hable del punto 1. Si actuando en forma mecánica lo hubiésemos hecho, el resultado habría sido un sistema de 6x6, y se podría contestar qué velocidad tenía la flecha al pasar por arriba del pino, cosa que el enunciado no pide. No lo hicimos porque la experiencia nos permite ir un poco más directamente al grano.

Aquí lo resolvemos, así te convencés de que no era difícil. De [1] despejo t₁

t₁ = 2 s

con este valor voy a [2] y calculo y₁: ésa es la altura máxima que puede tener el pino.

Me voy a [4] porque tiene una sola incógnita, debe ser fácil, pero fijate que justo la incógnita, t₂, aparece elevada al cuadrado. ¡Me cacho!... No es problema. Reacomodo la ecuación y la igualo a cero:

0 = – 8,75 m + 16 m/s . t₂ – 5 m/s² . t₂²

Me fijo bien en los coeficientes:

c = – 8,75 m,              b = 16 m/s,               a = – 5 m/s².

Y uso la salvadora:

Nuestra incógnita, t₂, va a tener dos resultados, uno usando el "+" y otro el "-".

t₂ = 0,7 s

t₂´ = 2,5 s

¿Cuál es el correcto? No hay forma de saberlo por ahora, pero podemos suponer provisoriamente que ambos son correctos y utilizar cada uno de ellos para calcular x₂, la posición del árbol.

x₂ = 12 m/s . 0,7 s = 8,4 m

x₂´ = 12 m/s . 2,5 s = 30 m

Como x₂, la posición del árbol, debe ser mayor (más lejana) que la del pino, podemos descartar que valga 8,4 m. Esto nos permite inferir que el instante en que se clava la flecha, t₂, es 2,5 s y no 0,7. La respuesta a la pregunta de cuánto duró el vuelo.

La velocidad de clavado, su módulo y ángulo. De [5] tenemos que

v_y2 = 16 m/s – 10 m/s² . 2,5 s = – 9 m/s

Esa es la componente vertical de la velocidad que buscamos. La componente horizontal es v_x, que vale 12 m/s, y no cambia... ¡es una constante! Para obtener el módulo de v₂ recurro al viejo Pitágoras.

Todavía falta el ángulo

α₂ = arc tg (v_y2/v_x) = arc tg – 0,75

DESAFIO: Primero: El arquero Gulderico arroja oblicuamente una flecha, la que parte desde una altura de 1,25 m, con una velocidad de 20 m/s y formando un ángulo de 53º con la horizontal. La flecha se clava horizontalmente en un árbol que se halla a cierta distancia. ¿Cuál es esa distancia? ¿Qué altura tiene, por lo menos, ese árbol?

Segundo: interpretar el significado del resultado de t₂ (0,7 s) que descartamos.