 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento uniformemente variado)
|
|

|
 |
NMS c3.39 - Un tren reduce uniformemente su velocidad, desde 12 m/s hasta 8 m/s, en una distancia de 100 m. Determinar su aceleración de frenado, y qué distancia recorrerá hasta detenerse si prosigue así. |
|
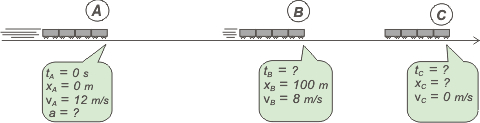
Como siempre lo primero es lo primero: un esquema. Vemos que en el problema aparecen tres puntos o situaciones diferentes: cuando el tren tiene 12 m/s, lo llamo A; cuando el tren tiene 8 m/s, lo llamo B y cuando el tren se detiene, lo llamo C... ¿Por qué no? Te lo hago en dos etapas, mirá.
|
 |
|
|
| Automáticamente surgen los nombres de todas las características -sean datos o incógnitas- que aparecen en el problema; de yapa queda establecido el SR. |
|
|
 |
|
|
Lo que sigue (en éste y en cualquier otro problema de cinemática) es armar las ecuaciones horarias. ¿Cuántas son? ¡Dos! Todo MRUV (y aquí hay uno solo) queda totalmente establecido con dos ecuaciones horarias, cuyos modelos son:
x = xo + vo ( t – to ) + ½ a ( t – to )²
v = vo + a ( t – to )
Por supuesto para armarlas hay que reemplazar las constantes (to, xo, vo y a). Lo más fácil es, para ello, elegir el punto A. Entonces queda: |
|
|
x = 12 m/s . t + ½ a t²
v = 12 m/s + a t
|
|
| Estas son las ecuaciones que describen TODO el fenómeno del movimiento delineado en el enunciado |
|
Mirá qué interesante... no pudimos reemplazar el valor de la aceleración porque no lo conocemos, pero bueno, es nuestro mejor proyecto de ecuación horaria; no nos achicamos y las escribimos igual, aún con una incógnita en el medio. Veremos que las ecuaciones horarias son unas herramientas tan potentes que aún así, "incompletas", resuelven solitas nuestros problemas.
Ahora... ¡las usamos! Es decir, les pedimos que hablen de aquellos puntos que para nosotros tienen interés ya sea porque hay datos o porque hay incógnitas: el B y el C (je, je, no hay otros). Si las ecuaciones hablaran del punto B dirían: |
|
|
 |
100 m = 12 m/s . tB + ½ a tB² |
|
| 8 m/s = 12 m/s + a tB |
|
|
|
Estas hablan sólo del punto B, que es el que a vos te interesa |
¡Alto!, ¡alto! Qué acabamos de escribir...: un sistema de dos ecuaciones con dos incógnitas (dos incógnitas que pedía el enunciado del problema). Esto tiene solución algebraica. ¡Aleluya, hermano! Ya hemos resuelto la mayor parte del problema: el resto es menos dramático. Hay muchos caminos para llegar a los resultados. Debe intentar cada uno el suyo... y recordar que esto es matemática, no física. Acá te muestro uno cualquiera, no es el más rápido ni el mejor.
Despejo a de la segunda ecuación:
a = ( – 4 m/s ) / tB
Reemplazo esto en la primera ecuación, y despejo tB.
100 m = 12 m/s . tB – 2 m/s tB
100 m = 10 m/s . tB
tB = 10 s
Para obtener a no necesitás ayuda. |
|
|
|
|
|
Una vez un estudiante, haciendo un esfuerzo por superar la timidez, se me acercó y me dijo: yo ya cursé la materia en otra aula y el profe nos había dado una fórmula complementaria que yo ponía las dos velocidades y aparecía la aceleración. Mi respuesta no se hizo esperar: ¡excelente! ¡Seguramente vas a poder encontrar fácilmente trabajo en una empresa de ferrocarriles!
Bueno, loco, sigamos con lo nuestro, que es ciencia (acá la cinemática y los trenes son sólo una excusa). ¿Y la distancia que recorre hasta detenerse? Pidámosles a las ecuaciones del movimiento que hablen del punto C. Ellas dicen: |
|
|
 |
xC = 12 m/s . tC + ½ a tC² |
|
| 0 m/s = 12 m/s + a tC |
|
|
|
Y éstas hablan exclusivamente del punto C, que también te interesa (supongo). |
¡Nuevamente un sistema de dos ecuaciones con dos incógnitas! (Ahora la aceleración ya sabés cuánto vale). ¡Qué inteligentes que son las ecuaciones! Ellas solas resuelven el problema. Lo que queda es pura álgebra. De la ecuación de abajo despejo tC
tC = 30 s
Con ese valor voy a la otra ecuación, y... |
|
|
|
|
|
Fijate que podríamos haber usado las ecuaciones de una, pidiéndoles que hablen de B y de C, sin hacer ningún cálculo, y nos hubiese quedado un sistema de 4X4, con solución algebraica. Ahí terminaba la física, el resto era álgebra. |
|
|
|
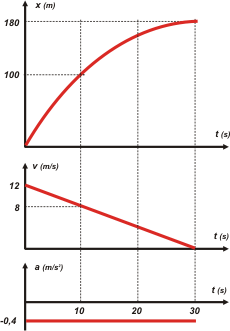
Por último los gráficos. Como siempre, los hago encolumnados, con la misma escala de tiempo y en un orden particular.
Observá qué inclinación le dibujé a la gráfica de posición (la parábola) en el último instante.
Ahora mirá un poquito el gráfico de velocidad. Forma un bonito triangulito con los ejes. Y la superficie de un triángulo era (bxh)/2, ¿te acordabas? Bueno, si hacemos el cálculo da 180 m... Igual que xC... ¡Qué casualidad!
Finalmente te pido que repares en esta correspondencia (de abajo para arriba): aceleración negativa, velocidad decreciente, parábola de concavidad negativa... |
|
|
DESAFIO: ¿qué tal si elegimos un SR orientado para el otro lado? ¿Qué resultados deben dar igual y cuáles distinto? |
|
 |
| Algunos derechos reservados.
O sea: los de propiedad intelectual, propiedad vertical y propiedad horizontal. Se permite su reproducción clonal citando la fuente. Última actualización abr-07. Buenos Aires, Argentina. |
|
|
| |
|

