 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA Y BIOFÍSICA
Ondas
|
|

|

|
Ejercicio 1.13 (modificado) - En un punto A de una cuerda de 2 m de longitud, se superponen dos ondas, armónicas procedentes de dos fuentes F1 y F2, en fase, situadas en los extremos de la cuerda. Sabiendo que ambas ondas se propagan con una velocidad de 40 m/s como indica la figura, con una frecuencia de 100 Hz cada una y con igual amplitud de 0,20 m, determinar la ecuación de movimiento oscilatorio que adquiere el punto A, que se halla a 0,55 m de F1. |
 |
|
|
No es difícil; prestá atención. Se trata de una onda estacionaria producida por dos viajeras idénticas excepto por el sentido de movimiento.
La velocidad y la frecuencia son datos aportados por el enunciado:
f = 100 Hz = 100 1/s = 100 s-1
v = 40 m/s
Y a partir de estos dos, podemos conocer la longitud de onda:
λ = v / f
λ = 40 m/s / 100 s-1
λ = 0,4 m
Se trata, obviamente de un armónico pequeño, ya que el armónico fundamental de la cuerda debe tener una longitud igual al doble de la cuerda ( λ1= 4 m ). Después podemos averiguar de qué armónico se trata, por ahora nos conforma saber que la cuerda vibra con 10 vientres ( 2L / λ ). Bien, ahora con estos datos vamos a calcular los parámetros de la onda estacionaria.
k = 2π /λ = 6,28 / 0,4 m = 15,71 m-1
ω = 2π . f = 6,28 . 100 s-1 = 628 s-1
A' = 2 A = 2 . 0,20 m = 0,40 m
Y teniendo el modelo correcto a mano, armamos la ecuación de la onda estacionaria. |
|
|
| |
y(t,x) = A' . cos ωt . sen kx |
este es el modelo |
| |
y(t,x) = 0,40 m . cos 628 s-1 t . sen 15,71 m-1 x |
y esta la ecuación |
|
|
|
Como ves, elegí el modelo en el que los ceros de x coinciden con los extremos de la cuerda (sen 0 = 0). A esta ecuación le pedimos que hable de la posición A, 0,55 m.
y(t,0,55m) = 0,40 m . cos 628 s-1 t . sen 15,71m-1 0,55 m
y(t,0,55m) = 0,40 m . cos 628 s-1 t . sen 8,64
y(t,0,55m) = 0,40 m . cos 628 s-1 t . 0,707
|
|
|
| |
y(t) = 0,28 m . cos 628 s-1 t |
|
|
|
|
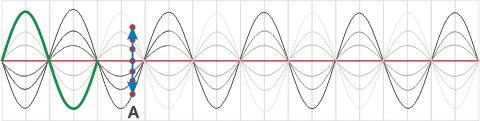
O sea, se trata de un punto (en rojo, en el siguiente gráfico) que oscila con una amplitud menor que la de la onda estacionaria. Miralo. |
|
|
 |
|
|
| Esa onda entera, dibujada en verde sobre el extremo izquierdo de la cuerda, te ayuda a revisar la escala del movimiento. La doble flecha azul representa la oscilación del punto A (en rojo), cuya ecuación de posición en función del tiempo obtuvimos en el ejercicio. ¿Te cierra? |
|
|
Desafío: ¿De qué número de armónico se trata? ¿Cuál es la ecuación de movimiento para un punto de la cuerda situado a 0,9 m? ¿Y la de otro situado a 1,2 m? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-09. Buenos Aires, Argentina. |
|
|
| |
|
|
|

