 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA DEL CBC
(Leyes de conservación)
|
|

|
TRABAJO de FUERZAS VARIABLES
Voy a presentar un modo de calcular el trabajo de fuerzas variables (como la fuerza elástica). Empecemos por presentar un tipo de gráfico bastante útil: nos muestra el valor de una fuerza, Fx, cualquiera en función de la posición -cambiante-, x, que ocupa un cuerpo.
|
 |
|
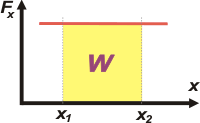
Se trata de un gráfico, como se ve, de fuerza en función de la posición. En este caso en particular se trata de una fuerza constante, tiene siempre el mismo valor, y el subíndice x indica que la fuerza tiene la misma dirección que la posición (y del desplazamiento).
Tomemos dos posiciones cualesquiera y llamémoslas x1 y x2. Y calculemos el "área encerrada baja la curva" entre ese par de posiciones. |
|
|
|
Acá tenés el área que vamos a calcular. Como se trata de un rectángulo es sencillo: lado por lado, base por altura. La base es igual a x2 — x1, y la altura es F. |
|
|
 |
|
Ese producto no es otra cosa que el trabajo de la fuerzaFx en el desplazamiento (x2 — x1).
WF = Fx . (x2 — x1) = Fx . Δx
De modo que el área encerrada bajo la curva de este gráfico es igual al trabajo de la fuerza. No se trata, claro, de un área geométrica. Es un área que representa una magnitud física, en este caso un trabajo. |
|
|
|
No se mide en unidades de superficie (m², cm², o cualquier otra). Se mide en unidades de trabajo, por ejemplo el joule, J. |
|
|
 |
|
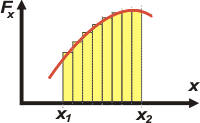
Aceptado esto, podemos preguntarnos si con las fuerzas variables (o sea, que cambia de valor en cada posición) pasa algo equivalente. La manera de obrar es la siguiente: fraccionemos el desplazamiento en pequeños segmentos.
El trabajo de la fuerza variable en el desplazamiento (x2 — x1) se aproxima mucho a la suma de los trabajos parciales representado por cada uno de los rectangulitos. |
|
|
|
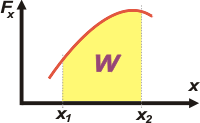
Pero esa aproximación se puede aumentar tanto como uno quiera haciendo cada vez más pequeños los segmentos de desplazamiento que después tendremos que sumar. |
|
|
 |
|
El análisis matemático permite hacer esas sumas de segmentos tan finitos que son invisibles. La notación es ésta:
W = ∫ Fx dx
Que se lee así: el trabajo es igual a la suma integral de todos los productos entre el valor de la fuerza y el pequeño segmento de desplazamiento durante el que actúa la fuerza. |
|
|
|
O un poco más crípticamente: el trabajo es igual a la integral de la fuerza por el diferencial del desplazamiento.
En los cursos iniciales de Física no se suele apelar a las habilidades ni a los conocimientos de análisis matemático de los estudiantes, y No me salen no lo hace. Pero sí a las habilidades geométricas, que son mucho más básicas. Ya que el cálculo de integrales es equivalente al cálculo de áreas. Por lo tanto tené presente esta conclusión que nos va a ser útil en la resolución de muchos ejercicios: |
|
| Si la palabra diferencial te genera mucha angustia te recomiendo leer este breve artículo. |
|
| |
| El trabajo de una fuerza, variable o no, es igual al área encerrada bajo la curva en un gráfico fuerza-posición entre dos posiciones cualesquiera. |
|
|
|
|
|
| Las áreas emplazadas sobre el eje de las posiciones representan trabajos positivos y se hallan debajo del eje de posiciones, trabajos negativos. |
|
|
CHISMES IMPORTANTES: |
|
|
- Por supuesto: no se puede integrar si se desconoce cómo varía la fuerza respecto a las posiciones, o sea, si se desconoce la función ƒ(F→ x). Pero no te preocupes, no te voy a pedir que resuelvas integrales; sí te voy a pedir que calcules áreas.
- Fue Newton -el creador del análisis matemático junto a Leibnitz- el que se dio cuenta que el cálculo de áreas era equivalente a la integración.
|
|
|
PREGUNTAS CAPCIOSAS: |
|
|
- ¿Te animarías a resolver la integral para una fuerza constante?
|
|


|
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-12. Buenos Aires, Argentina. |
|
|
|

