 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
dN3.13. ¿Por qué se inclina la bicicleta, la moto o cualquier otro bicho de dos ruedas cuando tomamos una curva? ¿Y por qué dobla la bicicleta cuando se inclina el ciclista? ¿Por qué si mientras dobla el ciclista está inclinado no se cae? ¿Debe girar su manubrio el ciclista para que la bici doble, o alcanza con que se incline?
|
 |
En el problema 1.47 de esta guía expliqué la relación entre el ángulo de inclinación del conjunto bici-ciclista cuando toma una curva. Conviene que comiences este estudio por ese ejercicio. En él hicimos un planteo sencillo en base a la ingeniosa consideración de asumir que el móvil era un cuerpo puntual. Si bien a partir de ese planteo encontramos muchas respuestas al problema de la curva inclinada... no podemos hallar todas.
En esta resolución vamos a considerar al ciclista y su bici como un ciclista con su bici, o sea, como un cuerpo extenso y rígido. Aunque un poquito más difícil (no mucho) vamos a poder encontrar más respuestas a este enigmático y atrayente fenómeno. |
|
|
|
| NOTA. Durante la resolución de este problema voy a utilizar los conceptos momento de una fuerza y cupla o par de fuerzas que habitualmente se estudian en el capítulo Estática del cuerpo extenso. |
|
|
| |
|
| Comentario, (podés saltearlo si estás apurado): Una vez, hace tiempo planteé este problema en un foro de discusión académica entre físicos, y fué ahí que descubrí que a ellos también, como al resto de los mortales les gusta romperse la crisma por dar vueltas en bici. La gran mayoría insiste en que es un problema dificilícimo, y en las resoluciones del problema -frecuentemente erróneas- incluyen momentos de inercia, masas inerciales, sistemas de referencia no inerciales, rotación de llantas, efectos trompo, precesiones, fuerzas no-inerciales, pseudofuerzas, fuerzas centrífugas, fuerzas giroscópicas, pseudo-verticales o verticales relativas. Y utilizan herramientas de cálculo complicadas como matrices o tensores. Mamma mía... |
|
|
Bueno, resolvamos el problema sin inventar nada nuevo, con nuestras herramientas del curso de mecánica general, clásica e inercial, apostólica y romana. Hice tres DCLs que representan la misma situación, un instante durante la curva del ciclista, como en la foto. El DCL 1 es el que representa más fielmente la situación real. |
|
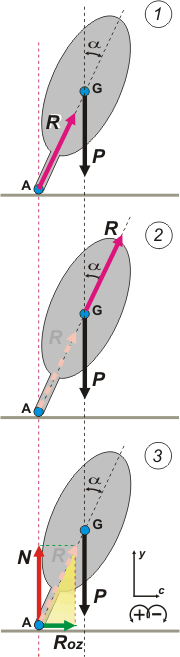 |
El peso del conjunto bici-ciclista, P, que como siempre es vertical y considerando al móvil un cuerpo extenso, actúa sobre el centro de masa o de gravedad, G.
Y hay una segunda fuerza que es la reacción del piso, R, que es una fuerza de contacto y que actúa, desde luego, sobre el punto de contacto, A. La dirección de R coincide con la inclinación del ciclista que que forma un ángulo α con la vertical. Esto puede no parecer obvio y merecedor de demostración, y la voy a hacer sobre el final.
El DCL 2 es muy parecido al 1. La única diferencia es que trasladé la fuerza R desplazándola sobre su recta de acción. Se trata de una operación vectorial conocida, sencilla, y válida para cuerpos rígidos como el de nuestro móvil (vamos a reservarle cierta flexibilidad al ciclista para que se lleve algunos laureles). Esta operación vectorial se asienta en nuestro entendimiento de lo que es un cuerpo rígido y sobretodo en la experiencia.
Lo interesante de esta operación es que nos remite a la resolución efectuada en la consideración de cuerpo puntual (problema 1.47), ya que hay sólo dos fuerzas... ¡y son concurrentes! La desventaja de esa operación es que no nos permite responder por qué el ciclista no se cae. Así que demos marcha atrás y volvamos a colocar a R en su punto de aplicación, A.
El DCL más interesante es el 3, porque nos pone de frente a fenómenos que desvelan a los físicos (no a los ciclistas) y que merecen respuesta.
Si descomponemos la reacción del piso en sus componentes vertical (apoyo propiamente dicho) y horizontal (rozamiento) -que llamé N y Roz respectivamente- vislumbramos el principal y paradojal conflicto que trastorna a los físicos.
Las fuerzas P y N son paralelas, de igual módulo y sentido opuesto. Este tipo de configuración se llama par, o cupla y tiene mucha importancia en la mecánica. Es obvio que provoca un torque, un giro, en esta caso negativo (según nuestra convención de signos) que tiende a hacer caer al pobre ciclista. ¿Qué es lo que imprime un giro contrario? ¿Qué es lo que hace que el ciclista no se caiga? |
|
|
Te adelanto la respuesta: lo que genera un torque en sentido contrario es el rozamiento, Roz, que hace que el ciclista no se caiga. Verán que no era para desvelarse. Vamos a la solución del ejercicios. Como en todo cuerpo extenso tendremos que se cumple la 2da. Ley de Newton y además la sumatoria de momentos valdrá cero.
ΣFc = m ac → R sen α = m v²/ r → Roz = m v²/ r
ΣFy = m ay → R cos α — P = 0 → N — P = 0 → N = P
ΣMG = 0 → MGP + MGR = 0
Dejemos la última (la de momentos) por un rato. A la aceleración centrípeta la reemplacé por su equivalente, v²/ r, donde r es el radio de la curva y v es la rapidez (módulo de la velocidad) del ciclista. Ahora metemos todo en la licuadora algebraica a ver si aparece algo interesante. Si dividimos miembro a miembro las dos primeras ecuaciones nos queda:
Roz / N = tg α
Ahora metemos la tercera y cuarta ecuación ahí adentro y llegamos
m v²/ r = m . g . tg α
|
|
| |
v² = r . g . tg α |
la discusión de este resultado está en 1.47 |
|
|
Claro, esto sólo vale si la inclinación del ciclista es la misma que la de R, la reacción del piso. Cosa que está por verse. De lo que no cabe duda es de que el ciclista no gira en el plano vertical, justo aquél en el que actúan las fuerzas. El ciclista sólo gira en el plano horizontal, por donde va el camino, que es lo que él quiere. De modo que la sumatoria de momentos de las fuerzas debe ser cero. Voy a tomar el punto G como centro de momentos. Cualquier otro es igualmente válido, pero G es el más sencillo y natural.
Como el momento de P vale cero ya que se aplica a G por naturaleza, al momento de R no le queda más remedio que valer cero debido a que la suma de ambos momentos debe ser nulo (si queremos que el ciclista no caiga al piso). El único modo de que R produzca un momento nulo respecto de G es que la recta de acción de R pase por G. O sea, que forme un ángulo α con la vertical. Así se justifica el razonamiento anterior, con el que realizamos las descomposiciones horizontal y vertical de R.
|
|
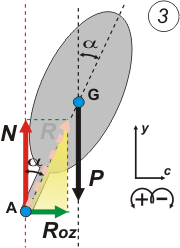
Todavía nos falta la explicación a la pregunta ¿por qué el ciclista no se cae al piso? Volvamos a la idea de momentos y trabajemos con las componentes de R, que son N y Roz.
Si llamo d a la distancia entre el punto de apoyo, A, y el centro de masa, G, entonces, mirando ahora el triangulito verde, la distancia entre las rectas de acción de N y P será igual a d sen α.
N y P forman una cupla que promueve el giro antihorario y que vale:
cupla N/P = — N . d . sen α
Se contrarresta con el momento de Roz, que promueve un giro horario igual a:
MGRoz = Roz . d . cos α
|
 |
|
|
Si recordamos quiénes son N y Roz, se ve que la cupla N/P vale lo mismo que
MGRoz.
cupla N/P + MGRoz = 0
— N . d . sen α + Roz . d . cos α = 0
— N . sen α + Roz . cos α = 0
— R cos α . sen α + R sen α . cos α = 0
— R + R = 0
Resumiendo: el ciclista no se cae porque la fuerza de rozamiento está aplicándole un torque que tiende a pararlo, y contrarresta el torque de su propio peso que tiende a acostarlo. Los ciclistas ya lo sabían... si un ciclista está tomando una curva y tiene la mala suerte de pisar una mancha de aceite no sólo deja de girar (y sigue de largo), también se cae al piso irremediablemente. |
|
Dicho en otras palabras, pese a que el ciclista está inclinado y cualquier hijo de vecino se caería en esa situación, ¿por qué el ciclista no cae? Porque esta sometido a la fuerza de rozamiento que empuja la parte de abajo de las ruedas hacia el lado de la inclinación provocando un torque (una fuerza de giro) igual y contrario al tirón de la gravedad. Se trata de un equilibrio bastante inestable (por eso se tarda un poco en aprender a andar en bici) pero está bastante ayudado por el diseño de la dirección del tren delantero (mirá el esquemita de abajo); el eje del manubrio (manillar) está un poco inclinado y retrasado del eje de la rueda. Eso permite andar sin manos y que la dirección de la bici responda a pequeños movimientos e inclinaciones que imprimimos con la cintura. Hay bicicletas más estables que otras.
Fijate que en esta resolución que hice no necesité apelar a ninguna fuerza extraña que no proviniese de una interacción común y silvestre; es el piso el que, empujando de costado, evita que el fulano caiga al piso.
La apelación común de muchos físicos a los efectos giroscópicos de las ruedas son despreciables e innecesarios. Este problema es absolutamente equivalente a otro más sencillo todavía en el que no hay ruedas ni efectos giroscópicos. Imaginate una regla paradita y haciendo equilibrio en el borde de un disco horizontal. Apenas una cinta scoch a modo de bisagra la sujeta al disco. Ahora el disco comienza a girar. La regla volteará hacia afuera. El único modo de encontrar un equilibrio y no caer ni hacia adentro ni hacia afuera es permanecer inclinada en un ángulo preciso que se calcula como lo hicimos con el ciclista. Ahhh... pero el ciclismo fascina a los físicos.
La segunda apelación rebuscada que hacen los académicos es la del movimiento de giro horizontal, o sea la curva que esta tomando el ciclista. Pretenden componer el giro horizontal (avance sobre la curva) con el supuesto equilibrio o no-equilibrio del giro vertical (caída). ¡Qué ganas de complicarnos la vida! El problema 1.11 de dinámica también es equivalente a éste, era el del péndulo colgado del techo de un vagón, y ahí no hay ningún giro horizontal. La aceleración del vagón es lineal. Si se considera al conjunto soga-masa como un cuerpo extenso (nada lo impide) o si prefieren reemplacen la soga por una varita rígida, entonces... ¿por qué no se hicieron esas preguntas paradojales antes? Es que les fascina romperse la cabeza con la bicicleta. |
 |
| |
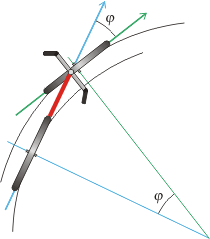
Otro mito que inspira la bicicleta es éste: ¿gira el manubrio cuando el ciclista toma la curva con la inclinación correcta? Hay textos que dicen que autos en peraltes o bicicletas con ciclistas inclinados no necesitan torcer la rueda para tomar la curva.
Ahí tenés un esquemita de un giro sin inclinación visto desde arriba. Es exagerado, pero sirve. Las ruedas siempre tienen su eje apuntando hacia el centro de la curva, y como están separadas sus direcciones de avance deben formar un ángulo idéntico al que forman sus ejes. La primera consecuencia de ésto es que el manubrio debe girar, las ruedas no pueden estar alineadas, tal como se observa claramente en la foto de arriba. Otra consecuencia de ésto es que las ruedas caminan sobre distintas circunferencias, hecho que queda al descubierto cuando giramos habiendo pisado un charco de agua. |
 |
|
|
 |
Son fenómenos casi imperceptibles. El esquema representa una curva con muy baja velocidad, si no, la bicicleta debería estar inclinada. Al aumentar la inclinación disminuye el ángulo de torción del manubrio y hasta puede hacerse cero (¡oh, sí!).
Pero yo invertiría la pregunta de esta manera: ¿puede un ciclista andar en bici con dos ruedas alineadas, es decir, sin poder girar la delantera? |
|
| Un colega mío -un tanto exótico- el maestro José Ciruela, desarrolló una explicación alternativa para el fenómeno de la inclinación de la bicicleta en las curvas. Se trata de una explicación absolutamente original y sorprendente, sobre todo, por su brevedad. Se encuentra publicada en este mismo sitio con el permiso del autor. |
|
|
| |
|
| DESAFIO: Una carrera la vuelta manzana, ¿dale? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ene-07. Buenos Aires, Argentina. |
|
|
|

