NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, fuerza de rozamiento)
|
|

|
NMS d3.08- Cuando un ciclista toma una curva en bici
sobre una pista horizontal (curva no peraltada)...
a- la inclinación que debe adoptar el ciclista ¿es tanto mayor cuanto mayor sea su peso?
b- la inclinación tiene que ver con la velocidad.
c- ¿De dónde proviene la fuerza centrípeta que
permite tomar la curva?
|
Este ejercicio puede ser muy, pero muy fácil... o muy pero muy difícil (y eso está por verse) según el camino que agarres con tu bicicleta. El modo difícil es el correcto y consiste en considerar al conjunto, ciclista-bici, como un cuerpo rígido y extenso, o sea, como lo es en la realidad. El camino sencillo es casi, casi, hacer trampa y considerar al móvil como un cuerpo puntual.
El modo tramposo es ya una costumbre en este curso de física, lo hemos aplicado hasta el cansancio y nos enorgullecemos de hacerlo. Todas las preguntas de este ejercicio se pueden responder satisfactoriamente con esta ingeniosa consideración, y como ejercicio adicional NMS D4 voy a resolver el problema correctamente y recién ahí vas a poder entender por qué te inclinás para pegar la curva. |
 |
|
|
|
Para que entiendas mejor el problema hice dos DCL en lugar de uno. El de la izquierda es el ciclista visto de frente cuando avanza en línea recta. El de la derecha es el que nos interesa, y es el ciclista doblando, que quedó bastante parecido al de la foto: se lo muestra también de frente y girando hacia nuestra derecha (la izquierda del ciclista).
El de la izquierda es muy sencillo. Hay sólo dos fuerzas actuando sobre el ciclista (vamos a suponer que todo el camino marcha con rapidez constante). Una de ellas es su propio peso, P, y la otra es la reacción, R, del piso, que en este caso es perpendicular al mismo y por eso lo llamé normal, N. R y N no son dos fuerzas diferentes, es la misma y es una sola... si no entendés eso no sigas. Si te cierra, dale para adelante, después te explico por qué le puse dos nombres diferentes a una misma fuerza. |
|
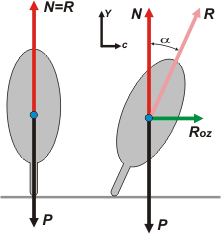 |
El DCL de la derecha es el de nuestro problema. Mientras gira en la curva actúan las dos mismas fuerzas que antes: su peso, P, que no ha cambiado, y la reacción del piso, R, que ahora está inclinada hacia el centro de giro (o sea hacia el lado de giro). Si le prestamos atención a R, la fuerza que hace el piso, vemos que al estar inclinada se puede descomponer en dos direcciones: una vertical y otra horizontal. La componente vertical (que en cualquier otro ejercicio lo hubiéramos llamado Ry) vale lo mismo que N al principio. La componente horizontal (que en cualquier otro ejercicio hubiéramos llamado Rx) es la que cambia la situación, es la responsable de que el ciclista pueda doblar. Rx es un rozamiento. |
|
|
La única deducción posible para esta aseveración (que no es otra que la pregunta c- del ejercicio) es experimental. Pero vos, que tenés bastante imaginación, podés darte cuenta que sería casi imposible pegar la curva sobre una mancha de aceite o sobre hielo. De algún modo tendrías que ingeniártela para lograr un "agarre" con el suelo porque si no seguirías de frente a estrolarte con el público. También podés asociar la idea con otras situaciones, como el aparentemente exagerado relieve que traen las cubiertas modernas de ruedas de bicicleta en las zonas laterales (las que se apoyan cuando estás inclinado), o simplemente con los problemas que ya resolvimos antes en los que giraban otros móviles que, si bien no se inclinaban, doblaban gracias al rozamiento.
Por último, debés tener claro que esa fuerza tiene la dirección y el sentido del centro de giro, o sea, es cetrípeta (cualidad geométrica). Y en cuanto a su naturaleza se trata de un rozamiento estático (¡no el máximo, es peligroso!), ya que no pretendemos (por nuestra salud y la de todos los ciclistas) que las ruedas deslicen sobre la curva sino que giren apoyándose firmemente cada milímetro que avancemos. |
|
| |
Fuerza centrípeta = Roze |
pregunta c - |
|
|
No se me escapa que tanto el rozamiento como el apoyo actúan en el punto de contacto entre la rueda y el piso mientras que el peso actúa sobre el centro de masa del móvil, cerca del ombligo del ciclista. Eso te prometo que lo asumiremos en el abordaje del NMS D4. Pero como por ahora se trata de un cuerpo puntual están todas las fuerzas actuando sobre el mismo punto.
De todos modos, la clave de este problema consiste en darse cuenta que el ángulo de inclinación, α, esta directamente relacionado con las componentes de la reacción en el apoyo.
Roz = R sen α
N = R cos α
Y si aplicamos la segunda ley de Newton
ΣFc = m ac → Roz = m v²/ r
ΣFy = m ay → N — P = 0 → N = P
A la aceleración centrípeta la reemplacé por su equivalente, v²/ r, donde r es el radio de la curva y v es la rapidez (módulo de la velocidad) del ciclista. Ahora metemos todo en la licuadora algebraica a ver si aparece algo interesante. Si dividimos miembro a miembro las dos primeras ecuaciones nos queda:
Roz / N = tg α
Ahora metemos la tercera y cuarta ecuación ahí adentro y llegamos
m v²/ r = m . g . tg α
la masa aparece de ambos lados del igual, así que la cancelo. Y acá está todo: |
|
|
|
| Si analizás este resultado podés responder las dos preguntas pendientes y muchas otras más. |
|
| |
la inclinación es independiente del peso del ciclista |
pregunta a - |
|
|
| |
cuanto mayor sea la velocidad mayor deberá ser la inclinación |
pregunta b - |
|
|
| |
|
| |
DISCUSION: El resultado parece muy sensato. Para empezar tiene las unidades correctas (nunca te olvides de chequear eso, tenés que convertirlo en una costumbre automática). Acordate que la función tangente vale 0 cuando α vale 0º. Y que crece infinitamente cuando α se acerca a 90º. Lo cual parece describir muy bien las curvas que pegan los ciclistas, motociclistas y cualquier otro ista que se desplace sobre superficies muy finitas... incluso los patinadores (perdón: patinadoristas).
La relación entre el radio de la curva y la inclinación también parece razonable, intuitiva. Fijate que son inversamente proporcionales, si crece una decrece la otra... tal como vos lo hubieras predicho. |
|
 |
| DESAFIO: ¿Cuál es la velocidad máxima a la que se puede tomar una curva de 20 m de radio sobre un asfalto con un coeficiente de rozamiento de 0,34 , y con qué inclinación habrá que hacerlo? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente, o sea, a bigotes. Última actualización ene-07. Buenos Aires, Argentina. |
|
|
|

