NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
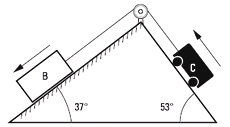
d2.13- En el sistema de la figura, el bloque B de
200 kg y el carrito C, también de 200 kg, se mueven
inicialmente en el sentido indicado, vinculados
entre sí por un cable que pasa por una polea,
estos últimos de masa despreciable.
Puede despreciarse el rozamiento en la polea
y entre el carrito y el plano en que se apoya, pero
entre el bloque B y el plano el coeficiente de
rozamiento dinámico es μd= 0,25.
|
a- Determinar el módulo y el sentido de la aceleración
que experimentan en ese instante, y la
intensidad de la fuerza que soporta el cable.
b- Con el sistema en movimiento, se corta el
cable. Determinar la nueva aceleración que experimenta
cada cuerpo, y describir en forma cualitativa
su movimiento. |
 |
|
|
|
Si el autor del problema no se enoja, voy a llamar β al ángulo de inclinación del plano en el que está apoyado el cuerpo B, y γ (gamma) al que está enfrente, que tiene apoyado al cuerpo C. Simplemente, eso nos va a permitir encontrar una expresión para un resultado más general.
Ok, vamos a los DCL. |
|
|
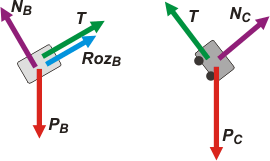 |
A las fuerzas de apoyo sobre los planos inclinados, NB y NC, las llamé normales para no tener conflictos gremiales.
La fuerza que hace la soga, T, es la misma sobre cada carrito ya que es una soga sin masa.
Todavía no puedo aplicar la Ley de la Masa porque las fuerzas no son codireccionales. |
|
|
|
| Rehagamos descomponiendo los pesos, y asignemos un SR coherente con una aceleración posible para el sistema. |
|
|
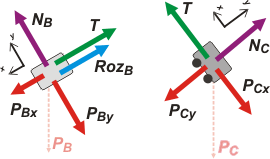 |
Descompuse las fuerzas peso:
PBx = PB sen β
PBy = PB cos β
PCx = PC sen γ
PCy = PC cos γ
Si te cuesta comprender estas relaciones te pido que le pegues una ojeada a esto. |
|
|
|
| Ahora las ecuaciones de Newton. Las aceleraciones son idénticas, porque la soga es inextensible. |
|
|
| |
Cuerpo B, eje x |
PBX — RozB — T = mB a |
[1] |
| |
Cuerpo B, eje y |
NB — PBy = 0 |
[2] |
| |
Cuerpo C, eje x |
T — PCX = mC a |
[3] |
| |
Cuerpo C, eje y |
NC — PCy = 0 |
[4] |
| Además de Newton podemos agregar lo que sabemos del rozamiento: |
| |
Cuerpo B |
RozB = μd NB |
[5] |
|
|
|
Si te tomás el trabajo de contar ecuaciones e incógnitas, verás que la física del problema se merece un descanso. Empieza un ejercicio de álgebra. No te lo voy a hacer, pero te cuento un camino más o menos rápido, ¿dale?
Sumás miembro a miembro la [1] con la [3]. En el primer miembro de la ecuación resultante se cancela T y en el segundo sacás factor común a. En lo que queda reemplazás el rozamiento por su igual sacados de [5]. En esta última que quedó reemplazás NB y NC por sus iguales despejados de [2] y [4]. Si me seguiste y hiciste bien habremos llegado acá. Fijate.
PBX — μd PBy — PCX = a (mB + mC)
ahora reemplazamos pesos por productos m . g y agrupamos por masas |
|
|
| |
| a = g |
|
mB (sen β — μd cos β) — mC sen γ |
|
|
| mB + mC |
|
|
|
|
|
Recién ahora hacemos números...
a = 10 m/s² [200 kg (0,6 — 0,25 0,8) — 200 kg 0,8 ] / 400 kg
a = 10 m/s² [200 kg ( 0,4 ) — 200 kg 0,8 ] / 400 kg
a = 10 m/s² [— 80 kg] / 400 kg
|
|
|
|
|
|
|
|
|
| La pregunta b) es muy sencilla, basta que nos remitamos al problema 2.16 y hagamos el cálculo individualmente para cada cuerpo. |
|
|
| |
|
 |
| DISCUSION: En el recuadro amarillo tenés una expresión general para discutir hasta el cansancio. |
|
| DESAFIO: ¿Cuánto debe valer el coeficiente de rozamiento para que el conjunto se deslice con velocidad constante? |
|
| Algunos derechos reservados.
Se permite su reproducción citando a ricuti, y decís que es el autor, claro. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

