NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
Plano inclinado con rozamiento
|
|

|
 |
dNMS2.12- Una chica de 50 kg desciende esquiando
por una pendiente que forma un ángulo de 37°
con la horizontal. El rozamiento con el aire es
despreciable y el coeficiente de roce dinámico
entre los esquíes y la nieve es de 0,25. Entonces
el desplazamiento realizado en tres segundos, a
partir del reposo, es:
a) 36 m ; b) 9 m : c) 12 m ; d) 18 m ; e) 24 m |
|
Más allá de que la mina esté refuerte, sea joven, hermosa y millonaria, no deja de ser un problema común y silvestre de plano inclinado con rozamiento.
Si querés entenderlo bien, antes tenés que repasar o recordar perfectamente el de plano inclinado sin rozamiento. Era el 1.10, andá y volvé, yo te espero.
Hagamos el DCL.
|
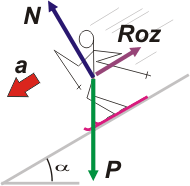 |
Acá tenés. Usé el mismo DCL de antes, pero le agregué la fuerza de rozamiento, Roz, que como te das cuenta es de tipo dinámico.
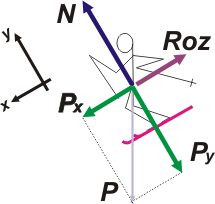
Del mismo modo que ocurrió en el otro, para poder aplicar Newton tenemos que elegir un SR y descomponer las fuerzas que no coincidan con las direcciones del SR elegido.
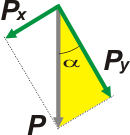
Vamos a descomponer el peso. (Por si no te acordás cómo se descompone un vector, te voy a ayudar con un esquemita:)
|
 |
Si mirás el triangulito amarillo podés ver que
Px = P sen α
Py = P cos α
|
Si no cazás por qué α es el que marqué en el esquema y no otro, te recomiendo que leas esta lección seria, aunque esté escrita en tono de chiste. |
|
|
|
Vamos a las ecuaciones. Empezamos por la dirección paralela al plano.
ΣFx = m ax = m a
Ahora hay dos fuerzas en esa dirección:
Px — Roz = m a
Qué ocurre en la dirección normal al plano:
ΣFy = m ay = 0
N — Py = 0
Acá se acaba Newton, pero nos queda una ecuación más por plantear, ya que conocemos la naturaleza de la fuerza de rozamiento y sabemos que:
Roz = μd . N
Ya con esto alcanza. Te paso en limpio las ecuaciones que tenemos y las numero, para que no te pierdas en el álgebra. |
|
|
Px — Roz = m a
N — Py = 0
Roz = μd . N
|
[1]
[2]
[3] |
|
|
|
En la [1] reemplazo Px por su igual, tal como lo vimos un poco más arriba.
P sen α — Roz = m a
Acá reemplazo Roz con su igual, según la [3]:
P sen α — μd . N = m a
Y en esta reemplazo N, según la [2]:
P sen α — μd . P cos α = m a
Expreso los pesos como m g:
m g sen α — μd . m g cos α = m a
La masa de la chica no importa (en este caso) pero convengamos que no está nada mal: 50 kgf es un buen peso.
g sen α — μd . g cos α = a
Saco factor común g y llegamos: |
|
|
|
|
|
¿Pudiste seguirme? Bueno, calculemos a y con eso vamos a la cinemática (MRUV) y sacamos el desplazamiento para 3 segundos. Δx = ½ a Δt²
a = 10 m/s² (0,6 — 0,25 . 0,8)
a = 4 m/s²
|
|
redondeemos:
sen 37° = 0,6
cos 37° = 0,8 |
|
|
|
| |
|
|
DISCUSION: El resultado que te recuadré en amarillo es el que hay que discutir. Fijate que si μd fuera cero, o sea si no hubiese rozamiento estaríamos en el mismo resultado que el problema 1.10, es un buen indicio. Si μd crece, la aceleración decrece, puede llegar a ser cero (la mina baja con velocidad constante, aprovechemos...) o incluso, si μd sigue creciendo podemos tener aceleración negativa, que en este SR significa que la mina se va frenando (para esperarme, obvio).
Fijate vos qué pasa variando α. Todo cierra. No dejes de hacer la discusión de los resultados... porque es la parte más importante de los ejercicios... y, como en mi caso, puede llegar a cambiarte la vida. |
|
 |
| DESAFIO: ¿Cuánto debe valer μd para que la mina baje a velocidad constante en una pendiente α cualquiera? |
|
| Algunos derechos sobre la esquiadora reservados.
Se permitió su reproducción sólo conmigo y, lógicamente, citando la fuente. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

