NO ME SALEN
SOLVED PHYSICS EXERCISES FROM THE CBC
Dynamic, linked bodies
|
|

|
Additional No me salen D1* - Find the value of force F for the block of mass m2 not slide on the inclined plane. Assume no friction between the inclined plane, the block and the floor.
|
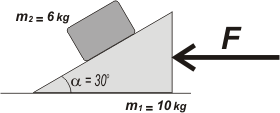 |
|
|
*This is a beautiful problem, by surprising and elegant. Also it seems to be pretty hard. It wasn’t taken to physics students in any exam, instead ¡it was part of a contest to choose teachers for physics! And the result was very regrettable… only a few applicants could resolve it, and between who couldn’t there were a lot of advanced students and professionals already graduated
I’m gonna take it as a paradigmatic example about how we resolve dynamics problems. From the habitual method and the No me salen method. First I’m going to develop the habitual method, reproducing a resolution that Agustin Rela brought, an admired and beloved friend and colleague, in an internal publication of matter.
HABITUAL METHOD
“You wonder which force applied to the set would make block not slip on the plane; supposing friction zero.”
“If the body does not slide supported, his motion is horizontal; in consequence it doesn’t accelerate vertically and there is no force net applied over it: It weight is balanced by the vertical component from the normal force to the plane that goes up and left”.
P2 = N cos α
N = P2 / cos α
“Knowing now N, it horizontal component to the left will be N sen a, and if the mass from the body it’s m2, it acceleration will be N sen α / m2.
"Con la aceleración se calcula con facilidad la fuerza exterior que se pide: |
|
|
| F = (m1 + m2) |
. |
P2 |
. |
sen α |
|
|
|
| cos α |
m2 |
|
|
|
F = (m1 + m2) . g . tg α
|
|
|
| |
F = 90,5 N ." |
(Agustín used g = 9,8 m/s²) |
|
|
|
Undoubtedly brilliant, just like Agustin, someone who I respect and admire. His resolution gathers all the characteristics from the habitual method that I also commented for cinematic. It's brief, concise, witty, with a minimum of algebra… almost magic. The author “got the way” to solve the problem, while many other colleagues that day on the exam tried to find that same way, but they couldn’t.
NO ME SALEN METHOD
Agustin himself, seeing my resolution he said: “…this alternative procedure, more orderly, methodical (¡you can not miss!) […] it is to make the separate free-body diagrams for the wedge and the block.” |
|
|
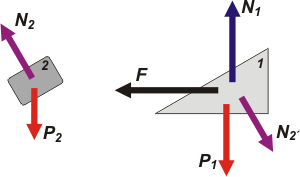 |
The forces acting upon the body 2 are: sthe weight, P2; the support over body 1, N2.
And upon body number 1: the weight, P1; the support over the floor, N2; the external force, F; and the force that the body 2 lmakes to the body 1 (the support), N2', which it is the pair of action and reaction with N2. |
|
|
|
| I’ll redoing decomposing those annoying forces oblique (which fortunately are a couple of action and reaction). As always, I choose the Frame of Reference having the direction x parallel to acceleration. |
|
|
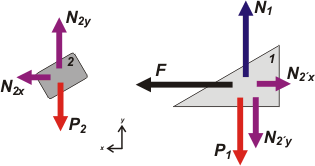 |
Consider:
N2x = N2 . sen α
N2y = N2 . cos α
Also:
P = m . g
|
|
|
|
| And the acceleration is the same for both bodies. Now, just like always, follows Newton’s equations. |
|
|
| Cuerpo 1 en x → |
ΣFx = m1 a |
→ |
F — N2x = m1 a |
[1] |
| Cuerpo 1 en y → |
ΣFy = 0 |
→ |
N1 — P1 — N2y = 0 |
[2] |
| Cuerpo 2 en x → |
ΣFx = m2 a |
→ |
N2x = m2 a |
[3] |
| Cuerpo 2 en y → |
ΣFy = 0 |
→ |
N2y — P2 = 0 |
[4] |
|
|
|
Do not bother counting… there are four equations and four unknowns. Here ends the physical and aspiring teacher would have approved. The rest is algebra and do not hesitate if they had been able to do the algebra, it is not something which would cause difficulty. To you maybe yes, for now, but I do like. There are about 3,572 different ways to solve this system. Here is one. (Equation [2] not going to need or will use).
Now let’s resolve. From [3] I clear a and replace N2x
a = N2 . sen α / m2
I put it on [1] and replace N2x
F — N2 . sen α = m1 . N2 . sen α / m2 [5]
From [4] I replace N2y and clear N2
N2 . cos α = m2 . g
N2 = m2 . g / cos α
I take that to [5]
F — m2 . g . tg α = m1 m2 . g . tg α / m2
In the second member you can cancel m2
F — m2 . g . tg α = m1 . g . tg α
F = m1 . g . tg α + m2 . g . tg α
F = (m1+ m2) . g . tg α
|
|
|
|
|
|
Agustin ends his commentary about my method saying: “The FBD is perhaps one of the most fruitful methodological tools of the mechanics”. |
|  |
Discussion: Check that not even me or Agustin replace one thing or fact until we made the final calculate once you get the expression of what the problem was asking. Always keep that on mind. |
|
Challenge: Find the other 3 unknowns missing. |
|
| Translated by
Lionel Vizcarra. Some rights reserved. You can reproduce quoting the source. Last actualization sep-06. Buenos Aires, Argentina. |
|
|
|

