NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
Dinámica, cuerpos vinculados
|
|

|
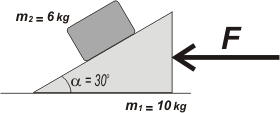
NMS 1.41* - Hallar el valor de la fuerza F para que el bloque de masa m2 no deslice sobre el plano inclinado. Suponga nulo los rozamientos entre el plano inclinado, el bloque y el piso.
|
 |
|
|
*Este es un problema hermoso, por sorprendente y elegante. Además parece ser bastante difícil. No fue tomado a los estudiantes de física en ningún examen, sino que ¡era parte de un concurso de selección de docentes para física! Y el resultado fue bastante deplorable... muy pocos aspirantes pudieron resolverlo, y entre los que no pudieron había muchos estudiantes avanzados y profesionales ya recibidos.
Yo lo voy a tomar como ejemplo paradigmático de cómo resolvemos los problemas de dinámica. Del método habitual y del método No me salen. Primero voy a desarrollar el método habitual, reproduciendo una resolución que brindó Agustín Rela, un admirado y entrañable amigo y colega mío, en una publicación interna de la materia.
EL METODO HABITUAL
"Se pregunta qué fuerza aplicada al conjunto haría que no deslice el bloque sobre el plano; los rozamientos se suponen nulos".
"Si el cuerpo apoyado no desliza, su movimiento es horizontal; en consecuencia no acelera verticalmente y no hay fuerza neta aplicada sobre él: su peso es equilibrado por la componente vertical de la fuerza normal al plano hacia arriba e izquierda".
P2 = N cos α
N = P2 / cos α
"Sabida ahora N, su componente horizontal hacia la izquierda será N sen α , y si la masa del cuerpo es m2, su aceleración será N sen α / m2.
"Con la aceleración se calcula con facilidad la fuerza exterior que se pide: |
|
|
| F = (m1 + m2) |
. |
P2 |
. |
sen α |
|
|
|
| cos α |
m2 |
|
|
|
F = (m1 + m2) . g . tg α
|
|
|
| |
F = 90,5 N ." |
(Agustín usó g = 9,8 m/s²) |
|
|
|
Indudablemente brillante, tal como lo es Agustín, a quien respeto y admiro. Su resolución reúne todas las características del método habitual que también comenté para cinemática. Es breve, conciso, ingenioso, con un mínimo de álgebra... casi mágico. El autor le "encontró la vuelta" al problema, mientras muchos colegas nuestros el día del examen en el concurso también "le buscaron la vuelta", pero no se la pudieron encontrar.
EL METODO NO ME SALEN
El propio Agustín, al ver mi resolución dijo: "...este procedimiento alternativo, más ordenado, metódico (¡no podés perderte!) [...] consiste en hacer los diagramas de cuerpo libre separados para la cuña y el bloque." |
|
|
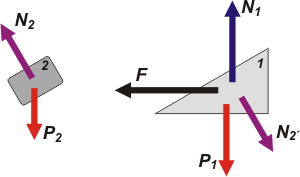 |
Las fuerzas que actúan sobre el cuerpo 2 son: su peso, P2; el apoyo sobre el cuerpo 1, N2.
Y sobre el cuerpo 1: su peso, P1; el apoyo sobre el piso, N2; la fuerza externa, F; y la fuerza que el cuerpo 2 le hace al 1 (el apoyo), N2', que es el par de acción y reacción con N2. |
|
|
|
| Los rehago descomponiendo esas fuerzas molestas oblicuas (que por suerte son un par de acción y reacción). Como siempre, elijo un SR que posee la dirección x paralela a la aceleración. |
|
|
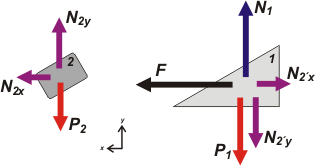 |
Tengamos en cuenta que:
N2x = N2 . sen α
N2y = N2 . cos α
Que:
P = m . g
|
|
|
|
| Y que la aceleración es la misma para ambos cuerpos. Y ahora, como siempre, siguen las ecuaciones de Newton. |
|
|
| Cuerpo 1 en x → |
ΣFx = m1 a |
→ |
F — N2x = m1 a |
[1] |
| Cuerpo 1 en y → |
ΣFy = 0 |
→ |
N1 — P1 — N2y = 0 |
[2] |
| Cuerpo 2 en x → |
ΣFx = m2 a |
→ |
N2x = m2 a |
[3] |
| Cuerpo 2 en y → |
ΣFy = 0 |
→ |
N2y — P2 = 0 |
[4] |
|
|
|
No te molestes en contar... hay cuatro ecuaciones y cuatro incógnitas. Acá terminó la física y los aspirantes a profesor hubieran aprobado. El resto es álgebra y no dudes que ellos habrían podido con el álgebra, no es algo que les crea dificultad. A vos tal vez sí, por ahora, pero yo te lo hago. Hay unos 3.572 caminos diferentes para resolver este sistema. Acá va uno. (La ecuación [2] no la voy a necesitar ni la voy a usar).
Ahora sí resolvamos. De [3] despejo a y reemplazo N2x
a = N2 . sen α / m2
Eso lo meto en la [1] y reemplazo N2x
F — N2 . sen α = m1 . N2 . sen α / m2 [5]
De [4] reemplazo N2y y despejo N2
N2 . cos α = m2 . g
N2 = m2 . g / cos α
Eso lo meto en la [5]
F — m2 . g . tg α = m1 m2 . g . tg α / m2
En el segundo miembro se puede cancelar m2
F — m2 . g . tg α = m1 . g . tg α
F = m1 . g . tg α + m2 . g . tg α
F = (m1+ m2) . g . tg α
|
|
|
|
|
|
| Agustín finalizaba su comentario sobre mi método diciendo: "el DCL es quizá una de las herramientas metodológicas más fecundas de la mecánica". |
|  |
| DISCUSION: fijate que ni Agustín ni yo reemplazamos un solo dato hasta no hacer el cálculo final una vez obtenida la expresión de lo que pedía el problema. Tenelo siempre en cuenta. |
|
| DESAFIO: Hallar las otras 3 incógnitas que faltan. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

