Este ejercicio tiene mucha tela para cortar. Arranquemos en una situación general e intermedia en la que la cadena tiene unos cuantos eslabones apoyados sobre la mesa y otros cuantos (no necesariamente el mismo número) colgando. No interesa si arranca del reposo o ya venía deslizando (sabés que la aceleración es la misma), lo que sí importa es que no hay rozamiento.

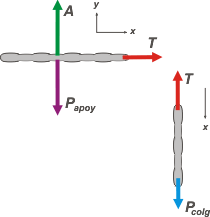
Se trata de una situación que ya practicamos en una buena cantidad de ejercicios (1.26, 1.29, 1.34 y otros), basta con imaginar a todos los eslabones apoyados como un sólo cuerpo, y a los eslabones colgando como otro cuerpo diferente, y la unión entre ellos como una unión sin masa pero inextensible, como si fuera una cuerda que ejerce una fuerza T idéntica en ambos extremos. El diagrama del cuerpo libre para esa situación es el siguiente:

Si tomamos en consideración el SR que representé al lado de cada DCL, las ecuaciones de Newton dirán:

eslabones apoyados  →        ΣF = m_apoy . a    →                 T = m_apoy . a

eslabones colgantes  →        ΣF_x = m_colg . a   →      P_colg — T = m_colg . a

El peso de la tira colgante es igual a su masa por la aceleración de la gravedad. Y además, si suponemos que todos los eslabones son idénticos y que tienen la misma masa, entonces, la masa de cada tira será igual al producto de la masa de un eslabón, m_e, por el número de eslabones de cada porción, n. Por último: las aceleraciones de ambas tiras son idénticas, ya que la cadena (o nuestra soga sustituta) son inextensibles.

Hechas esas aclaraciones, sumemos miembro a miembro las ecuaciones de Newton de cada tira.

a  = g . m_e . n_colg / m_e . n_apoy + m_e . n_colg

a  = g . m_e . n_colg / m_e . ( n_apoy + n_colg )

a  = g . m_e . n_colg / m_e . n_total

La masa de un eslabón aparece multiplicando en el numerador y en el denominador, de modo que se cancela, y nos queda...

a_n  = g . n_colg / n_total

Esta descripción es muy clara y sencilla: cuando apenas cuelga un eslabón la aceleración será pequeña (por ejemplo si en total hay 20 eslabones y uno sólo colgando, la aceleración valdrá 1/20 g), cuando esté la mitad colgando y la mitad todavía sobre la mesa, la aceleración valdrá g/2, y cuando ya no quede ningún eslabón sobre la mesa, la aceleración será igual a g. Resumiendo: la aceleración va cambiando en función de la cantidad de eslabones que hay arriba y abajo, por eso le agregé un subíndice, a_n, que remarca esa dependencia.

Un resultado muy intuitivo y hasta predecible. Ya podemos dar la primera de las respuestas.

La segunda pregunta ofende la inteligencia humana. No la vamos a contestar. En cambio, vamos a hacer algo mucho más divertido y productivo: vamos a meditar sobre la variación de la aceleración.

La magnitud que describe los cambios de aceleración se llama tirón (jerk en inglés), y lo voy a simbolizar así: j. El tirón habrá que medirlo en unidades de aceleración divididas unidades de tiempo, por ejemplo:

[j] = m/s³

Se trata de una magnitud física muy interesante que tiene varias aplicaciones en mecánica, sobre todo en aquellos casos en los que hay que medir "violencia" que deben resistir objetos, materiales, personas.

Un movimiento de tirón uniforme tendría estas ecuaciones horarias (para t_o = 0).

x = x_o + v_o t + ½ a_o t²+ (1/6) j t³

v = v_o + a_o t + ½ j t²

a = a_o + j t

j = cte

Pero... ¿nuestra cadena se moverá con tirón constante o con tirón variado? ¿Querés pensarlo sin mi ayuda o te lo cuento?

El tirón de la cadena cambia cada vez que un eslabón pasa de la tira apoyada a la tira colgante, y el pasaje es cada vez más rápido, de modo que no ocurre en forma uniforme. Queda para vos encontrar las ecuaciones horarias para la cadena.