 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, polea simple, cuerpos vinculados)
|
|

|
| |
 |
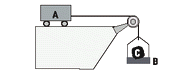
FIS d1.21 - En el sistema de la figura, suponiendo
conocidas las masas mA, mB y mC y despreciando
las masas de cuerda y polea, así como todos
los rozamientos, hallar las expresiones de: |
 |
|
a- La aceleración de A.
b- La fuerza que ejerce la cuerda.
c- La fuerza de contacto entre B y C.
d- Explicar por qué sobre A actúa horizontalmente
una fuerza cuya intensidad es menor que
la suma de los pesos de B y de C.
e- Si mB + mC >> mA, analizar y tratar de predecir,
sin hacer cálculos, la aceleración del sistema. |
|
Este problema es muy parecido al anterior, y me interesa sobremanera compararlos. Pero hay un problema... que en lugar de haber un cuerpo colgando hay dos: el B y el C. Esto tiene solución: lo voy a resolver como si fuese un problema diferente y al finalizar voy a hacer la siguiente consideración: que los cuerpos B y C estan unidos y forman uno sólo BC de masa mBC (de todas maneras, aunque haya una fuerza entre ellos, no se separan en todo el viaje; todos los cuerpos poseen fuerzas interiores, y eso no representa problema alguno). Va de suyo que: mBC = mB + mC
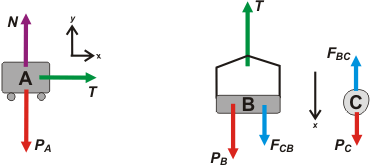
Vamos a hacer el DCL, esta vez una sola tanda alcanzará. Nuevamente la ecuación vertical de A no aporta gran cosa, ni la escribo. |
 |
|
|
Cuerpo A → ΣFx = m a → T = mA . a
Cuerpo B → ΣFx = m a → PB + FCB — T = mB . a
Cuerpo C → ΣFx = m a → PC — FBC = mC . a
Casi lo mismo que antes. Sumamos las tres ecuaciones miembro a miembro
T + PB + FCB — T + PC — FBC = mA . a + mB . a + mC . a
PB + PC = a . (mA + mB + mC)
|
|
|
| |
a = g . ( mB + mC ) / ( mA + mB + mC ) |
la a) del enunciado |
|
|
|
Para hallar el valor de la tensión de la cuerda basta reemplazar esta de aceleración en cualquiera de las ecuaciones iniciales... más fácil en la primera. |
|
|
| |
T = g . mA . ( mB + mC ) / ( mA + mB + mC ) |
la b) del enunciado |
|
|
|
Para hallar la fuerza de contacto voy a la tercera ecuación
mC . g — mC . a = FBC
mC . g — mC . [ g . (mB + mC) / (mA + mB + mC) ] = FBC
no te pierdas ahora ¿eh? Tomátelo con tranquilidad y resolvelo solo. Suma de fracciones, ¿remember? |
|
|
| |
FBC = g . mA mC / (mA + mB + mC) |
la c) del enunciado |
|
|
|
| Las últimas te la dejo a vos y no protestes. Vamos a lo que a mí me interesa. Fijate la respuesta a) y apliquemos la transformación mBC = mB + mC |
|
|
| |
a = g . mBC / ( mA + mBC ) |
|
|
|
|
| Mirá es la misma respuesta que se obtiene en el ejercicio 1.20 para α = 0º . Y es la misma de problema 1.25 y así , una generalización de muchos problemas básicamente iguales que se relacionan unos con otros por las inclinaciones y las distribuciones de las masa. |
|
|
| |
|
|
DISCUSION: Del mismo modo que discutimos las otras se pueden discutir cada una de las expresiones que obtuvimos como resultado en cada una de las preguntas de este problema.. Verificando que concuerden las unidades, y discutiendo intuitivamente el funcionamiento del sistema vos, además de aprender un toco de buena física, podes estar seguro de que resolviste bien, sin tener que revisar 500 veces el álgebra, las ecuaciones ni nada. La expresion describe... escuchá esa descripción, si dice cosas sensatas es correcta si dice cosas estúpidas, entonces algo anda mal.
Te tiro un ejemplito: decime vos sin mirar ninguna expresión de las que obtuvimos, ¿cuánto debe valer la fuerza de contacto entre B y C si la masa de A valiese cero, o lo que es lo mismo, si se corta la cuerda? OK, ahora andá y buscá la expresión que te lo certifica, andá, está por allá arriba. |
|
 |
| DESAFIO: Que respondas la pregunta d) |
|
| Algunos derechos son reservados, y algunos zurdos son extrovertidos.
Se permite su reproducción (entre zurdos y diestros) citando la fuente. Agradezco a Juan Carlos Costa por el envío de una errata . Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

