NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, cuerpos vinculados)
|
|

|
| |
 |
FIS d1.18 - En los tres sistemas que se proponen a
continuación, puede despreciarse el rozamiento
con el plano y en la polea, y las masas de las
cuerdas y la polea. La intensidad de la fuerza
aplicada es igual al peso del cuerpo 2.
|
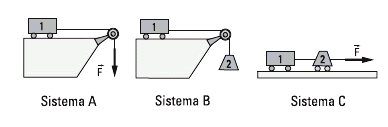 |
a- Comparando los sistemas A y B, analizar
cualitativamente (sin hacer cálculos) cuál se
mueve con mayor aceleración.
b- Repetir el análisis anterior, comparando
ahora B con C.
c- Suponiendo ahora que la intensidad de la
fuerza F es 5 kgf, y que la masa del cuerpo 1 es
20 kg, calcular las respectivas aceleraciones y verificar
las predicciones hechas anteriormente. |
|
Este es un excelente ejercicio, fundamental, aleccionador. No podés dejás de analizarlo en detalle si querés aprender algo de Física. Podría empezar por las lecciones. Pero prefiero resolverlo como si fuese un ejercicio común y silvestre... y reservarme la lección fundamental para el final. Voy a resolver solamente los casos A y B. Ya vas a ver por qué.
De modo que el método tradicional exige empezar por los DCL. En el caso A es uno solo. Acá va. |
|
|
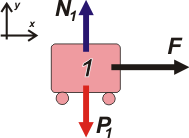 |
Hay varias cosas que observar. Primero, las sogas que nosotros usamos son sogas "sin masa", eso garantiza que las fuerzas que realizan en ambos extremos son iguales. Y la poleas que usamos tampoco tienen masa, y sólo sirven para cambiar la dirección de las sogas. Todo eso me permite reemplazar la fuerza que hace la soga sobre el carrito 1 por la fuerza F que se ejerce en el otro extremo. |
|
|
|
Segundo: en el eje y no hay aceleración (el carrito no levanta vuelo ni se hunde en el piso), de modo que la aceleración del sistema sólo ocurre en la dirección x y la voy a llamar aA. La ecuación de Newton habla de ella:
ΣFx = m1 aA → F = m1 aA
Podemos calcularla:
aA = 50 N / ( 20 kg )
|
|
|
|
|
|
| Ahora vamos al caso B (es un clásico). Tenemos que hacer dos DCLs. |
|
|
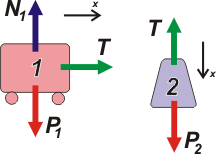 |
Fijate que adopté para ambos cuerpos un SR coherente (la dirección de movimiento, sea cual sea tendrá el mismo signo).
Para el cuerpo 1 no cambia casi nada, solo que ahora tira de el la soga, T, que es la misma que sostiene al cuerpo 2.
Naturalmente, se vienen las ecuaciones de Newton. |
|
|
|
Cuerpo 1 → ΣFx = m1 ax → T = m1 aB
Cuerpo 2 → ΣFx = m2 ax → P2 — T= m2 aB
Hay dos ecuaciones con dos incógnitas. De modo que podemos calcular la aceleración. Un método sencillo y rápido es sumar miembro a miembro las dos ecuaciones y luego despejar aB'.
aB = P2 / ( m1 + m2 )
aB = 50 N / 25 kg
Sorpresa: |
|
|
|
|
|
Lo paradójico de la comparación es que la fuerza externa que mueve al sistema en ambos casos vale lo mismo: 50 N (en un caso es F y en el otro es P2). Sin embargo la segunda aceleración es menor.
La explicación es sencilla (y se supone que tenés que ser capaz de cazarla al vuelo, por eso el enunciado pide que respondas sin hacer cálculos). En un caso -el A- una fuerza mueve una cierta masa. En el otro -el B- la misma fuerza (cantidad de fuerza) tiene que mover una cantidad de masa mayor... y por eso logra una aceleración menor.
Si entendiste el significado de esa proposición, vas a poder predecir correctamente la aceleración del caso C sin hacer cálculos.
Esta idea (la que surge de la comparación en este ejercicio) es fundamental en la Física, porque nos presenta a las fuerzas como las productoras de aceleraciones y a las masa como la resistencia a ser acelerados.
Sin ir más lejos, tenés acá la explicación de por qué los cuerpos -independientemente de sus masas y pesos- caen siempre con la misma aceleración. (Un hito en la historia de la Física). Si un cuerpo pesa más está más fuertemente atraído hacia abajo, sin embargo no logra más aceleración, porque, en la misma proporción, también tiene más masa.
Mirá qué curioso. |
|
|
| |
|
|
| DESAFIO: Obvio, microbio... que respondas las preguntas que le quedan al ejercicio. |
|
 |
| |
| Algún derecho quedó sin reservar.
No se permite su reproducción sin citar la fuente. Ojito. Última actualización ene-11. Buenos Aires, Argentina. |
|
|
|

