NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, vínculos)
|
|

|
| |
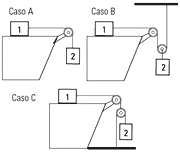
| FIS d1.25 - Calcular la aceleración de los cuerpos 1 y 2
y la tensión en las sogas en cada caso.
Considerar las sogas y poleas como ideales, y
despreciar el rozamiento entre el cuerpo 1 y la
superficie horizontal.
Primero resolver algebraicamente y luego
analizar el movimiento para m1 = 4 kg y m2 = 6 kg. |
 |
|
| |
|
|
El caso A, ya lo resolviste 78 veces, en varios ejercicios FIS 18, FIS 21. Igualmente te presento el resultado de este caso ya que va a ser interesante compararlo con los otros dos: |
|
| |
a = 6 m/s² , T = 24 N |
Caso A |
|
|
|
| Vamos con el caso B que se pone más interesante: |
|
|
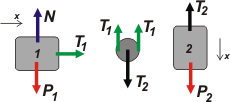 |
T1 = m1 . a1
T2 — 2 T1 = 0
P2 — T2 = m2 . a2
El error típico cuando planteamos estas ecuaciones en los ejercicios de este tipo consiste en olvidar que las aceleraciones son diferentes. |
|
|
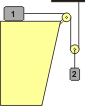 |
Si no te olvidás de eso, entonces podés sumar una ecuación más, ya que no es difícil razonar que cada vez que el cuerpo 1 avanza un trecho, el 2 baja medio trecho, ¿te cierra? Entonces:
a1 = 2 a2
Ahora sí, metemos todo eso en la licuadora algebraica...
|
|
|
| a2 = g . |
|
m2 |
|
|
| ( m2 + 4 m1 ) |
|
|
|
| |
a1 = 5,45 m/s² a2 = 2,72 m/s² T1 = 21,8 N |
Caso B |
|
|
|
| Vamos al Caso C... (que estoy seguro que ya lo podés resolver sin ayuda). |
|
|
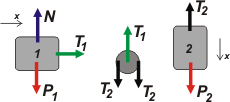 |
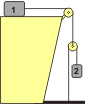
Parece casi idéntico al anterior, pero la diferencia aparece en la polea:
T1 = m1 . a1
2 T2 — T1= 0
P2 — T2 = m2 . a2
Y fijate que en el mismo tiempo que el cuerpo 2 avanza un trecho, el cuerpo 1 avanza medio trecho, de modo que:
2 a1 = a2
|
|
|
 |
Vamos al álgebra: |
|
|
| a1 = g . |
|
2 m2 |
|
|
| ( m1 + 4 m2 ) |
|
|
|
| |
a1 = 4,28 m/s² a2 = 8,56 m/s² T1 = 17,1 N |
Caso C |
|
|
|
| DESAFIO: ¿Es posible que en los 3 casos el cuerpo 2 esté subiendo? |
|
 |
| Algunos derechos reservados, otros no.
Se permite su reproducción citando la fuente. Agradezco a Erick Osorio por el envío de una errata. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
|

