NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, polea simple, cuerpos vinculados)
|
|

|
| |
 |
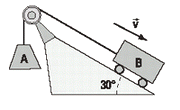
FIS d1.20 - En el esquema de la figura, los bloques A
de 60 kg y B de 40 kg se mueven en el sentido indicado,
vinculados por una cuerda flexible e
inextensible de masa despreciable. Puede despreciarse
también el rozamiento sobre el plano y
en la polea, y la masa de esta última. |
|
 |
a- En las condiciones dadas, hallar la intensidad
y sentido de la aceleración de los bloques, y
la fuerza que soporta la cuerda.
b- Se corta la cuerda en la situación planteada
en la figura. Calcular la nueva aceleración de cada
uno.
c- Describir el movimiento de cada bloque
desde el instante inicial hasta que lleguen al piso.
Esbozar los gráficos posición-tiempo. |
|
|
| Un clásico de los clásicos, y vamos a tratar de relacionarlo con otros clásicos. Ya vas a ver. Empecemos por los DCLs. |
|
|
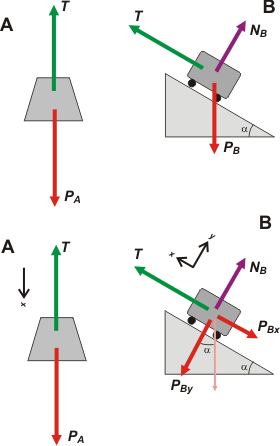 |
El par éste, de arriba, es el original, el que te ayuda a pensar las fuerzas como las interacciones que son.
El par de abajo son los operativos, los que te ayudan a plantear las ecuaciones dinámicas. La única diferencia es que en el segundo siempre vas a encontrar fuerzas paralelas u ortogonales, y provienen de haber descompuesto algunas fuerzas, las que no coinciden con las direcciones del SR que hayas elegido.
Elegir correctamente el SR es toda una habilidad que se aprende con la práctica... lo más común es usar la dirección x paralela y con sentido homogéneo para la aceleración. |
|
|
|
Bueno, vamos entonces a las ecuaciones.
Cuerpo A → ΣFx = m ax → PA — T = mA . a
Cuerpo B → ΣFx = m ax → T — PBx = mB . a
ΣFy = m ay → NB — PBy = 0
La tercera ecuación no aporta gran cosa en este problema. En esa dirección el bloque B no acelera, ya que ni levanta vuelo ni se hunde en el plano. Pero las dos primeras ecuaciones sí dicen, y bastante.
Fijate que PBx = PB . sen α, por si tenías dudas... ahí te volví a dibujar α, entre PBy y PB , ¿lo tenés? Bueno, ahora sí hagamos un poco de álgebra.
Si sumo miembro a miembro las dos primeras ecuaciones tengo...
PA — T + T — PBx = mA . a + mB . a
PA — PB . sen α = a . (mA + mB)
g . mA — g . mB . sen α = a . (mA + mB)
g . (mA — mB . sen α ) = a . (mA + mB)
|
|
| Si te cuesta entender el asunto de la descompo-sición de la fuerza peso, te recomiendo leer este apunte. |
|
| |
a = g . (mA — mB . sen α ) / (mA + mB) |
|
|
|
|
|
|
|
| (Mirá qué significa que nos haya dado positivo: que el conjunto se está frenando, ¿no?). Bueno, las otras dos preguntas te las dejo a vos, porque sí. ¡Y andá a protestar a la superintendencia de la re%$·@·#&¾^$%*ª! |
|
|
| |
|
|
DISCUSION: No me salen siempre te recuadra los resultados en gris (porque somos muy serios, viste)... la expresión recuadrada en amarillo es mucho más interesante que el resultado numérico. Vamos a sacarle un poco de provecho, y a disfrutarlo. Veamos. Lo primero que trato de mirar en una expresión como ésa... lo más fácil de mirar, es si posee las unidades correctas... y efecticamente las tiene. Después me pregunto qué me dice... por ejemplo si α vale 90º, sen α vale 1, y fijate que nos queda exactamente el mismo resultado que el problema 1.32, que ya hicimos. Si α vale 0º, sen α vale 0, y obtendríamos el resultado del problema 1.34, o 1.29... o sea, con uno de los cuerpos apoyado en un plano horizontal. En fin, la expresión esa dice mucho, mucho más, describe la mecánica del sistema. Podés preguntarle que pasa si la masa de uno de los cuerpos se hace despreciable (0), y seguir jugando así. Ahí aprendés Física. Tenés una variante más de este mismo problema acá. |
|
 |
| DESAFIO: Hallar una expresión para el valor de la tensión de la cuerda. Hallar qué condición debe cumplirse para que la aceleración valga cero. |
|
| Unos cuantos derechos reservados, no te vayas a creer...
Eso sí, se permite su reproducción (y la tuya, claro está) citando la fuente. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

