 |
NO ME SALEN
APUNTES TEÓRICOS Y EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
|
|

ac = ω² . R
ac = v² / R
ac = ω . v
ac = 4π² ƒ² R
ac= 4π²R /T²
ac = 2π v / T
ac = 2π v ƒ |
Dinámica del movimiento circular
Para claridad de la exposición voy a comenzar describiendo la dinámica de un movimiento circular uniforme, MCU, y sobre el final me referé a los movimientos circulares no necesariamente uniformes y a cualquier otro movimiento curvilíneo. Acá vamos:
Como recordarás los móviles que describen circunferencias (o arcos de circunferencia) están acelerados hacia el centro de la circunferencia. Y a esa aceleración la denominamos aceleración centrípeta, ac, que se puede calcular en base a diferentes parámetros cinemáticos (en el margen hay una lista de diferentes formas, todas equivalentes entre sí).
Y acá viene el concepto fundamental: si en esta situación aplicamos el 2do. principio de la denámica (2da. Ley de Newton) escribiremos:
ΣF = m ac
Como esta ley nos muestra una igualdad vectorial debemos concluir que la sumatoria de las fuerzas, ΣF, también apunta hacia el centro de la circunferencia, o sea, la sumatoria de fuerzas, o si vos querés, la resultante, es centrípeta.
ΣF = Rc = m ac
Y recíprocamente: si sobre un cuerpo actúan fuerzas cuya resultante apunta permanentemente hacia un punto, ese cuerpo tendrá una aceleración centrípeta y se moverá con un MCU. Acá va un esquema sencillo que describe lo dicho. |
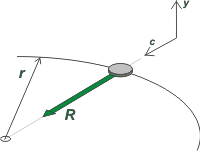 |
Ojo que está es perspectiva, o sea, la trayectoria dibujada es un arco de circunferencia, de radio r. La fuerza neta que actua sobre el móvil mientras se mueva sobre una trayectoria circular y a velocidad angular constante debe, necesariamente, apuntar hacia al centro de la circunferencia. Luego, esa resultante, R, es centrípeta.
En última instancia, ser o no ser centrípeto es una característica de tipo geométrico, y significa que apunta permanentemente hacia un punto: el centro de la circunferencia. |
|
|
|
Cuando necesites aplicar la segunda ley y precises un sistema de referencia es muy conveniente que uno de los ejes apunte hacia el centro de la circunferencia. A ese eje se lo suele llamar, c, pero es solo una costumbre, podés llamarlo x si te resulta más familiar. Alguien puede objetar que c es un eje que sirve sólo para un instante, ya que al toque la aceleración del cuerpo adopta otra dirección, pero no importa para nada, ya que la dinámica refleja instantáneas del universo, no describe procesos. Tu eje sirve para esa foto y con eso alcanza y sobra.
Severas confusiones
Lamentablemente muchos estudiantes (y no pocos docentes, profesores, físicos e ingenieros) olvidan que R es una resultante, una sumatoria de fuerzas, no es -necesariamente- una interacción verdadera. De ahí surge el mito -falso- de la existencia misteriosa de fuerzas centrípetas y el de la inexistencia de fuerzas centrífugas.
Miremos este ejemplo: |
|
|
 |
|
Ser o no ser centrípeto es una característica geométrica, no implica una naturaleza especial.
Cualquier fuerza puede, en alguna situación ser centrípeta, y por qué no también, centrífuga. |
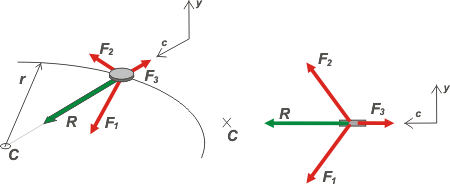
A la izquierda en perspectiva y a la derecha visto de canto. Sobre el cuerpo actúan tres fuerzas, F1, que apunta un poco hacia abajo, F2, que apunta un poco hacia arriba, y F3 que apunta en sentido opuesto al centro de la circunferencia, C. ¡Ninguna apunta hacia el centro! ¡No hay ninguna fuerza centrípeta! !Incluso hay una fuerza centrífuga!
La que necesariamente es centrípeta si el movimiento es circular uniforme, es la resultante, R (en verde), que no es una interacción con otro cuerpo.
Moraleja: no te olvides de que la segunda ley de Newton no habla de cada una de las fuerzas que actúan sobre un cuerpo, sino de la resultante de todas ellas, que no es -necesariamente- una interacción, una fuerza cabalmente hablando. (La resultante es una interacción sólo cuando es la única fuerza que actúa sobre un cuerpo). |
|
|
 |
|
|
| Pibes girando uniformemente en el tiovivo. Describen circunferencias perfectas, sin embargo ninguna fuerza centrípeta actúa sobre ellos. |
|
|
|
Si querés leer más sobre este asunto de las fuerzas centrípetas y centrífujas podés ir a esta lección de mi maestro, el Maestro Ciruela.
Circulares no-uniformes y curvilíneos
Cuando un cuerpo avanza sobre un trayectoria circular variando no sólo la dirección sino también el módulo de la velocidad, su movimiento ya no será uniforme, y la aceleración no apuntará al centro de giro si no un poco inclinada hacia donde se produce el aumento de velocidad. En esos casos (no voy a profundizar mucho sobre el tema) es muy conveniente descomponer la aceleración en estas dos direcciones: una centrípeta (normal a la trayectoria) y otra tangencial a la trayectoria. Mirá el esquema: |
|
|
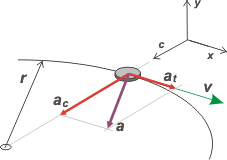 |
En morado la aceleración, sus componentes en rojo y la velocidad en verde.
La componente centrípeta, ac, describe el cambio de dirección; la componente tangencia, at, describe el cambio de rapidez; y la aceleración verdadera, a, tendrá la misma dirección y sentido que la resultante de las fuerzas que actúan sobre el cuerpo... as allways. |
|
|
|
| Una conclusión intreresante de lo que antecede es que la aceleración de un cuerpo siempre apunta hacia el lado interno de la curva que recorre. |
|
|
| CHISMES IMPORTANTES: |
|
|
- Un caso muy común de error en el planteo de las fuerzas (y por lo tanto en la resolución de ejercicios) es el del péndulo cónico. Sobre la masa actúan sólo dos fuerzas: la que hace el piolín y el peso. Ninguna de las dos es centrípeta (ninguna de las dos apunta hacia el centro de giro). Entonces muchos estudiantes agregan una fuerza: la centrípeta... ¡que no existe!
- La velocidad de un móvil siempre es tangente a la trayectoria.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|
 |
- ¿Qué es el círculo osculatriz?
- ¿Qué es un sistema de referencia no-inercial?
- ¿Qué es una pseudofuerza?
|
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-15. Buenos Aires, Argentina. |
|
|
 |
|

