 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, péndulo cónico)
|
|

|
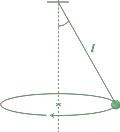
NMS d3.14* - Suponga un péndulo cónico como se muestra en la figura. La cuerda es inextensible y de longitud 1 m. La masa es de 1 kg y el ángulo que forma la cuerda con la vertical es de 30°.
- ¿Cuánto vale la tensión de la cuerda cuando la masa está girando?
- Si en algún momento se corta la cuerda, ¿Con que velocidad sale disparada la masa?
|
 |
|
*Este ejercicio formó parte del 2do. examen parcial tomado el 11-11-2011. |
|
|
 |
Como todo ejercicio de dinámica... ya sabés por dónde hay que empezar.
Acá está el DCL, describiendo las dos únicas fuerzas que actúan sobre el péndulo cuando se halla en la misma posición que te lo dibujé en el esquemita. La fuerzas son; el peso de la masa, P; y la tensión con que lo tira la cuerda, T. |
|
|
|
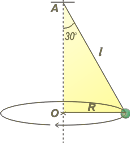 |
Hagamos algunas aclaraciones sobre el esquema del péndulo que me parece que son pertinentes y que después vamos a necesitar.
Cosas destacables del esquema. La circunferencia que describe el péndulo es horizontal y tiene su centro en O (¡no en A!), y su radio R.
Bueno, tenemos que escribir las ecuaciones de Newton, pero, como las fuerzas no son co-direccionales, debemos descomponer una de ellas. Lo más práctico es descomponer T. Acá va el nuevo DCL. |
|
|
|
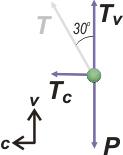 |
Recordás que siempre que enfrentás un MCU a uno de los ejes lo llamás c (por centrípeto), en lugar de x, ¿no? Es cierto que se trata de un eje que va cambiando con el tiempo. Pero no te olvides que la dinámica son sólo instantáneas del universo. Fijate que α = 30º (dos paralelas cortadas por una transversal generan ángulos alternos internos que son iguales entre sí, jijiji...) y eso permite establecer que:
TV = T . cos 30°
Tc = T . sen 30° |
|
|
|
Ahora sí, vamos a Newton. En el eje vertical tenemos que la aceleración es cero (la circunferencia de la trayectoria no cambia de altura, está quieta).
ΣFv = 0 → TV — P = 0 → TV = m . g [1]
ΣFc = m ac → Tc = m ac → Tc = m v²/R [2]
El resto es una pavada: en la ecuación [1] reemplazás TV por su igual T . cos α y ya tenés la primera pregunta del enunciado:
T . cos 30° = m . g
T = m . g / cos 30°
T = 1 kg . 10 m/s² / cos 30°
|
|
 |
|
|
|
De la ecuación [2] despejás v, que es la velocidad tangencial con la que se mueve la masa, y es la velocidad con la que se va de paseo y se corta la cuerda.
T . sen 30° = m v²/R
Tené en cuenta (mirando el triangulito sombreado en el esquemita de arriba) que
R = l . sen 30°
Juntamos todo...
T . sen 30° = m v²/ l . sen 30°
Despejamos v
v² = T . sen 30° . l . sen 30° / m
v² = T . sen² 30° . l / m
v² = 11,55 N . sen² 30° . 1 m / 1 kg
|
|
|
|
|
|
|
|
 |
| DESAFIO: ¿Cuál es el error más frecuente en la resolución de los ejercicios de péndulo? |
|
| Algunos derechos, zurdos y ambidiestros reservados.
Se permite su reproducción citando la fuente. De los ambidiestros también. Última actualización nov-11. Buenos Aires, Argentina. |
|
|
|

