NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
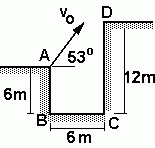
NMS c5.22*- Desde la orilla A del pozo esquematizado en la figura se arroja una piedra en forma
oblicua con velocidad inicial Vo, formando un ángulo de 53º por encima de la horizontal.
a.- Determinar la velocidad inicial máxima para que golpee en la pared
b.- Hallar la velocidad (expresar en componentes) en el instante del impacto. |
 |
|
¡¡¡Ehhh!!! No es para tanto... vas a ver que al final era tan difícil y tan fácil como cualquier otro problema de cinemática. Empecemos por entender de qué se trata: la incógnita del ejercicio es la velocidad inicial, v0, de la piedra. Si es muy alta pasa por arriba de D y vaya uno a saber a quién golpea. ¿Cuál será el valor máximo que puede tener esa velocidad para dar contra el muro y no pasarse? Si sale despedida con esa velocidad que estamos buscando, pegará en el muro... pero justo en D.
NOTA: en la segunda versión de este mismo ejercicio se pedía la velocidad mínima. El razonamiento es similar, y en este caso la piedra debe caer justo en C.
Ahora que está aclarado el asunto empecemos, como siempre, por el esquema. |
|
|
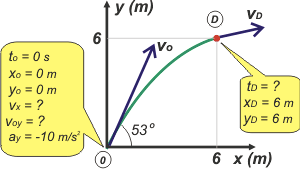 |
Notarás que la parte del pozo no nos interesa para nada. Coloqué los ceros del SR en el punto de partida de la piedra, y desde ahí hay 6 m para la derecha y otros 6 m para arriba para llegar a D.
No te olvides que: vx = v0 cos α0, y v0y = v0 sen α0
Ni tampoco que cos 53° = 0,6 y que sen 53° = 0,8 |
| |
|
Ok, que no haya pánico, vamos a armar las ecuaciones. Tomamos las constantes iniciales del movimiento y ya.
x = v0 0,6 . t
y = v0 0,8 . t – 5 m/s² . t²
vy = v0 0,8 – 10 m/s² . t
Ahora les pedimos a estas 3 ecuaciones que describen todas las posiciones y velocidades del proyectil, que hablen exclusivamente de la única posición que nos interesa, o sea, D. |
|
|
| |
6 m = v0 0,6 . tD |
[1] |
| 6 m = v0 0,8 . tD – 5 m/s² . tD² |
[2] |
| vyD = v0 0,8 – 10 m/s² . tD |
[3] |
|
|
Estas son las ecuaciones especializadas para el instante que a vos te interesa. |
Si mirás las dos primeras ecuaciones encontrarás un sistema de 2x2... o sea, con solución algebraica... y podremos decir cuánto vale v0.
Me imagino que querrás que yo lo haga. De la [1] despejo tD.
tD = 6 m/ v0 0,6
tD = 10 m/ v0
eso lo meto en la [2]. Controlá que no me equivoque:
6 m = v0 0,8 . (10 m/v0) – 5 m/s² . (10 m/v0)²
simplifiquemos un cacho
6 m = 8 m – 500 m³/s²/ v0²
– 2 m = – 500 m³/s²/ v0²
de donde
v0² = 250 m²/s²
|
|
|
|
|
|
Y si te interesa saber cuánto vale tD, volvés a la ecuación [1] y obtenés:
tD = 0,63 s
Bueno, resulta que además nos piden las componentes de la velocidad en D, o sea, las componentes de vD.
La componente horizontal se mantiene constante de modo que valdrá lo mismo que la componente horizontal inicial: vx = v0 cos 53°
vx = 15,8 m/s 0,6 = 9,5 m/s
Para conocer la componente vertical debemos recurrir a la ecuación [3]
vyD = 15,8 m/s 0,8 – 10 m/s² . 0,63 s = 6,35 m/s
|
|
|
| |
vD = ( 9,5 m/s ; 6,35 m/s ) |
|
|
|
|
| No fue tan dramático. |
|
|
| |
|
 |
| |
|
*Este ejercicio fue parte del examen parcial tomado el 08-05-2012.
|
|
| Desafío: ¿cuánto valdrá la velocidad mínima inicial para que la piedra golpee la pared? |
|
| Algunos derechos reservados.
Si en el básquet quieres encestar, no pierdas tiempo en plantear ecuaciones, sólo usa tu intuición y habilidad. Se permite su reproducción citando la fuente. Última actualización ene-12. Buenos Aires, Argentina. |
|
|
| |
| |
|

