NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
| NMS c5.21*- Un proyectil es lanzado formando un ángulo α con la horizontal. La distancia horizontal que recorre hasta caer en el suelo es tres veces la altura máxima alcanzada. ¿Cuál es el ángulo de tiro? |
|
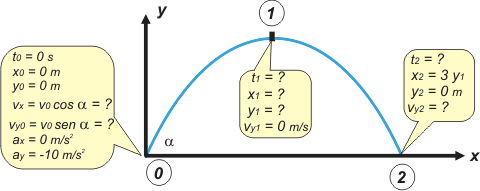
Parece que se complica, ¿no?... no desesperes... el suicidio siempre es la última opción. Antes, probemos el método No me salen; vas a ver que al final era tan difícil y tan fácil como cualquier otro problema de cinemática. Empecemos por el esquema.
No te olvides que dado un vector y el ángulo que forma con x, hay que considerar dato también a sus componentes: v0x = vx = v0 cos α, y v0y = v0 sen α |
|
|
| |
|
Ok, que no haya pánico, vamos a armar las ecuaciones. Tomamos las constantes iniciales del movimiento y ya.
x = v0 cos α . t
y = v0 sen α . t – 5 m/s² . t²
v = v0 sen α – 10 m/s² . t
Ahora les pedimos a estas 3 ecuaciones que describen todas las posiciones y velocidades del proyectil, que hablen exclusivamente de las posiciones de interés, que son la 1 y la 2. |
|
|
| |
x1 = v0 cos α . t1 |
[1] |
| y1 = v0 sen α. t1 – 5 m/s² . t1² |
[2] |
| 0 m/s = v0 sen α – 10 m/s² . t1 |
[3] |
| 3 y1 = v0 cos α . t2 |
[4] |
| 0 m = v0 sen α . t2 – 5 m/s² . t2² |
[5] |
|
|
Estas son las ecuaciones especializadas para los instantes que a vos te interesan. |
La ecuación de velocidad para el punto 2 no la usé porque nada nos dicen ni nos preguntan sobre esa velocidad... así lo hago menos pesado. Tampoco voy a necesitar la ecuación [1] ni la [5], pero contémoslas.
Quedó un sistema de 5 ecuaciones con 6 incógnitas. Ayudame a contar las incógnitas: α, que es la que nos interesa, x1, v0, y1, t1 y t2. Estamos en problemas. El único modo de salir de esto es usar uno de los argumentos de simetría de las trayectorias parabólicas: el tiempo que tarda en recorrer la primera mitad es igual al tiempo que tarda en recorrer la segunda mitad: |
|
|
|
|
|
Ahora sí, 6 contra 6: partido ganado. Todos los problemas son iguales... las ecuaciones horarias son herramientas muy poderosas. Hasta acá llegó la física... y el resto es ágebra. Si llegaste hasta acá tenés que estar contento: la física tiene reservado un lugar para vos. Bueno, te hago el álgebra es largo y trabajoso... pero no es física, es sólo álgebra (acordate que hay 368.944 caminos diferentes, y no te garantizo que el mío sea el más corto).
Reemplazo [6] en la [4] |
|
|
| |
3 y1 = 2 v0 cos α . t1 |
[7] |
|
|
|
De la [3] despejo t1 |
|
|
| |
t1 = v0 sen α / 10 m/s² |
[8] |
|
|
|
| Eso lo meto en la [2]. |
|
|
| |
y1 = (v0² sen² α – ½ v0² sen² α) / 10 m/s² |
|
| |
y1 = ½ v0² sen² α / 10 m/s² |
[9] |
|
|
|
| Y también en la [7] |
|
|
| |
3 y1 = 2 v0² sen α cos α / 10 m/s² |
[10] |
|
|
|
| Ahora multiplico la [9] por 3 y la resto con la [10] |
|
|
| |
0 = – (3/2) v0² sen² α + 2 v0² cos α sen α |
|
|
|
|
No te pierdas, este último paso te tiene que llevar por lo menos 3 renglones en tus apuntes para poder seguirme. Ahora viene lo mejor: saco factor común v0² sen α. |
|
|
| |
0 = – (3/2) sen α + 2 cos α |
|
| |
(3/2) sen α = 2 cos α |
|
| |
tg α = 4/3 |
|
|
|
|
Ahora le pido a la calculadora que me diga cuánto vale α |
|
|
|
|
|
| |
|
|
OBSERVACIÓN: No te pido que verifiques el resultado haciendo reemplazos en las ecuaciones anteriores... porque vas a perder más tiempo que reolviendo el álgebra de este ejercicio. (y además, nuestro resultado vale para cualquier valor de v0). Pero lo que podés hacer es inventarte una velocidad inicial cualquiera y, usando el ángulo que acacamos de hallar, verificás que el alcance es el triple de la altura máxima.
También podríamos haber usado otra de las características de la simetría de la parábola: 2 x1 = y2, pero ni la necesitamos, como ves se trataba de un ejercicio en el que sobraban muchos datos, aunque no nos hubieran dado ninguno. |
|
 |
| |
|
| *Este ejercicio bellísimo me lo envió mi amigo Raúl Marano Rodríguez desde Mendoza. |
|
| Desafío: si el proyectil es lanzado con la misma velocidad inicial que el nuestro, pero con un ángulo β = (90° – α) ¿cuánto valdrá su alcance? |
|
| Algunos derechos reservados.
Si en el básquet quieres encestar, no pierdas tiempo en plantear ecuaciones, sólo usa tu intuición y habilidad. Se permite su reproducción citando la fuente. Última actualización ene-12. Buenos Aires, Argentina. |
|
|
| |
| |
|

