NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo, encuentro)
|
|

|
| NMS c5.18* - Al disparar una bala de 50 g, con un ángulo de 30° hacia arriba respecto de la horizontal, se acierta a un blanco a 300 m de distancia y 40 m de altura con respecto a la boca del cañón. Calcule: a) el módulo de la velocidad con la que impacta en el blanco. b) la máxima altura alcanzada por el proyectil. |
|
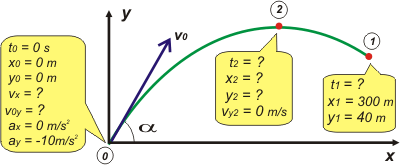
Parece un poco largo, ¿no?... es cierto, lo es... pero si somos pacientes y metódicos vas a ver que no es difícil. Empecemos, como siempre, por el esquema.
No te olvides que dado el ángulo que la velocidad inicial forma con x, sus componentes serán: v0x = v0 cos 30°, y v0y = v0 sen 30°... |
|
|
| |
|
Llamé 1 la situación de la que nos hablan primero, cuando el proyectil da en el blanco, y 2 la del punto más alto. Vamos a armar las ecuaciones. Tomamos las constantes iniciales de cada movimiento y ya.
x = v0 cos 30° . t
y = v0 sen 30° . t – 5 m/s² . t²
vy = v0 sen 30° – 10 m/s² . t
Ahora le voy a pedir a las ecuaciones que hablen del punto 1. |
acordate que
cos 30° = 0,866
sen 30° = 0,5 |
 |
300 m = v0 . 0,866 . t1 |
[1] |
| 40 m = v0 . 0,5 . t1 – 5 m/s² . t1² |
[2] |
| vy1 = v0 . 0,5 – 10 m/s² . t1 |
[3] |
|
|
Estas son las ecuaciones especializadas para el instante que nos interesa. |
¿Viste?, tanto drama... quedó un sistema de tres ecuaciones con tres incógnitas. Todos los problemas son iguales... las ecuaciones horarias son herramientas muy poderosas. Bueno, te hago el álgebra:
de la [1]
t1 = 300 m / v0 . 0,866
t1 = 346 m / v0
eso lo meto en la [2] |
|
|
| 40 m = |
|
v0 . 0,5 . 346 m |
– 5 m/s² ( |
346 m |
)² |
|
|
| v0 |
v0 |
|
|
|
| |
|
|
| 40 m = 173 m |
|
– 5 m/s² ( |
120.000 m² |
) |
|
| v0² |
|
|
|
| |
|
|
| –133 m = |
|
– 5 m/s² . 120.000 m² |
|
|
| v0² |
|
|
|
De ahí:
v0² = 4.512 m²/s²
v0= 67,17 m/s
No te habrás perdido, ¿no? Con eso voy de vuelta a la [1]...
t1 = 5,15 s
Con estos resultado voy a la ecuación [3]...
vy1 = 17,92 m/s
por otro lado, ya sabemos que
vx1 = vx = v0 cos 30° = 58,17 m/s
Para conocer el módulo de la velocidad con la que el proyectil da en el blanco, v1, podemos utilizar el Teorema de Pitágoras
v1 = (vx1² + vy1²)1/2
|
|
exponente ½
es lo mismo que
raíz cuadrada |
|
| |
v1 = 60,86 m/s |
quedé agotado. |
|
|
|
Todavía nos falta la segunda parte... esto es más largo que esperanza de pobre... Hay que pedirle de nuevo a las tres ecuaciones que describen el movimiento que hablen, ahora, del punto 2.
Te repito el esquema... que ya te olvidaste de qué se trataba: |
|
|
 |
|
|
 |
x2 = v0 . 0,866 . t2 |
[4] |
| y2 = v0 . 0,5 . t2 – 5 m/s² . t2² |
[5] |
| 0 m/s = v0 . 0,5 – 10 m/s² . t2 |
[6] |
|
|
|
Ahora es más fácil, porque ya sabemos cuánto vale v0= 67,17 m/s. Le vamos a pedir a la ecuación [6] que nos calcule t2...
t2 = 3,36 s
con ese valor nos corremos hasta la ecuación [5] y listo. |
|
|
| |
y2 = 56,3 m |
la altura máxima |
|
|
|
| Esta vez no te hago los gráficos porque son demasiado fáciles. |
|
|
| *Este ejercicio perteneció al examen parcial de Física tomado en Ciudad Universitaria el 19 de mayo de 2009. |
|
|
|
| DESAFIO: Livianito... que si llegaste hasta acá debés estar con una fisura atroz: ¿a qué distancia del cañón alcanza la altura máxima?... y hacer los gráficos. |
|
 |
| |
|
| Algunos derechos reservados.
Leer con moderación. Prohibida su venta a menosres de 18 años. Se permite su reproducción citando la fuente. Última actualización may-09. Buenos Aires, Argentina. |
|
|
| |
| |
|

