NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo, encuentro)
|
|

|
 |
NMS c5.10- Desde un punto en el suelo se lanza una
piedra con una velocidad de 5 m/s en una dirección
que forma un ángulo de 37° con la horizontal.
Simultáneamente desde otro punto se deja
caer una piedra, chocando ambas a los 0,3 s de
haber sido lanzadas. |
|
a - ¿Cuáles son las coordenadas del punto de
encuentro?
b - ¿Desde qué altura se dejó caer la segunda
piedra?
c - Realice las gráficas de x, y, vx, vy, en función
del tiempo para ambas piedras.
d - Dibuje en escala las trayectorias de ambas
piedras (en el mismo gráfico). Compare el ángulo
de tiro con el de mira.
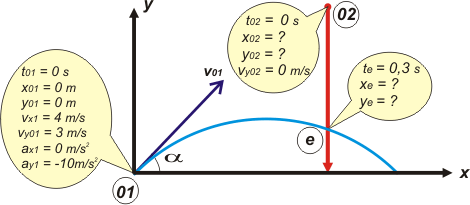
Parece que se complica, ¿no?... no desesperes... el suicidio siempre es la última opción. Antes, probemos el método No me salen; vas a ver que al final era tan difícil y tan fácil como cualquier otro problema de cinemática. Empecemos por el esquema.
No te olvides que dado un vector y el ángulo que forma con x, hay que considerar dato también a sus componentes: v01x = v01 cos 37°, y v01y = v01 sen 37° |
|
|
| |
|
Ok, ahí donde se cruzan ocurre el encuentro. Vamos a armar las ecuaciones. Tomamos las constantes iniciales de cada movimiento y ya. A las ecuaciones de velocidad les damos vacaciones ya que el problema no pregunta ni afirma nada sobre las velocidades en el encuentro.
Para la piedra 1 (tiro oblicuo)
x = 4 m/s . t
y = 3 m/s . t – 5 m/s² . t²
Para la piedra 2 (caída libre)
y = y02 – 5 m/s² . t²
Ahora les pedimos a estas 3 ecuaciones que describen todas las posiciones que hablen exclusivamente del encuentro. |
|
|
 |
xe = 4 m/s . 0,3 s |
[1] |
| ye = 3 m/s . 0,3 s – 5 m/s² . 0,09 s² |
[2] |
| ye = y02 – 5 m/s² . 0,09 s² |
[3] |
|
|
Estas son las ecuaciones especializadas para los instantes que a vos te interesan. |
¿Viste?, tanto drama... quedó un sistema de tres ecuaciones con tres incógnitas. Todos los problemas son iguales... las ecuaciones horarias son herramientas muy poderosas. Bueno, te hago el álgebra:
de la [1]
xe = 1,2 m
de la [2]
ye = 0,9 m – 0,45 m = 0,45 m
|
|
|
| |
E: ( 1,2 m î ; 0,45 m ĵ) |
las coordenadas del punto de
encuentro |
|
|
|
Por último vamos a la [3], de donde despejo y02
y02 = 0,45 m + 0,45 m
|
|
|
| |
y02 = 0,9 m |
altura inicial de la segunda
piedra |
|
|
|
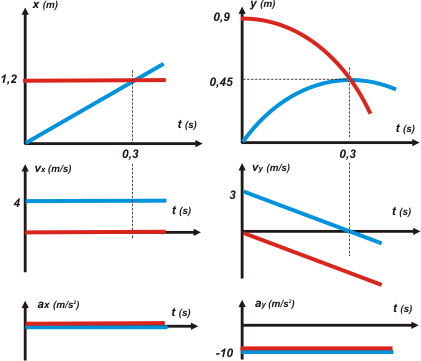
| Para hacer los gráficos en escala hay que calcular algunas cositas más. Con lo que tenemos no alcanza. Por ejemplo... cuál fue la altura máxima del tiro oblicuo, o cuándo la alcanzó. Si hacés ese cálculo te vas a encontrar con que la altura máxima se alcanzó justo a los 0,3 s, justo en el encuentro. No tiene ningún significado físico, es sólo falta de imaginación del autor del problema. Bueno, ahora sí podemos hacer los gráficos. |
|
|
 |
|
|
| DESAFIO: Bueno, rehacé vos el esquema... pero a escala, y fijate si hay alguna relación entre los ángulos que te digo ahora: el que forma la recta que une los puntos iniciales de ambas piedras, el del tiro oblicuo y el que forma la recta que une el inicial del tiro oblicuo con el punto de encuentro... Vos buscá... después hablamos. |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco A Camila Varela por el envío de una errata. Última actualización set-06. Buenos Aires, Argentina. |
|
|
| |
| |
|

