|
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
 |
NMS c3.42 - Two rams (a white and a black one) stand in front of each other, at a rest position, 24 m apart. In a given moment, both begin running towards each other. Considering constant accelerations of 1,6 m/s² y 1,4 m/s² respectively, determine the position in which their collision takes place, and the speed of each ram at that instant. Outline the correspondent graphs for position and velocity as a function of time. |
|
A horny problem indeed! Let´s not give in to fear, though: our kinematic tools are so powerful that no exercise will stand a chance. Let´s begin by representing the situation:
|
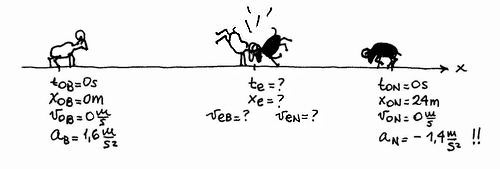 |
(This is an original NO ME SALEN drawing, nice, huh?) |
Take a look at the sign of the black ram´s acceleration: how would it have changed, had the chosen RS (Reference System) been set with an opposite sense? And, in that case, what would have been of the white ram´s acceleration?
It´ll be of your own best interest to have the kinematic equations for accelerated motion at hand, since we´re about to make use of them: |
|
|
 |
x = xo + vo ( t – to ) + ½ a ( t – to )²
v= vo + a ( t – to ) |
|
|
Let´s write down the equations that describe the motions of both rams. How many are they? Two for the black one, two for the white one, for a total of four. In order to find them, we´ll just need to replace the constants in the general equations (to, xo, vo y a) with the initial constants of each ram. |
|
|
| White: |
x = 0,8 m/s² . t²
v = 1,6 m/s² . t |
|
These are the equations that describe THE WHOLE situation proposed in this exercise. |
| Black: |
x = 24 m – 0,7 m/s² . t 2
v = – 1,4 m/s² . t |
|
And now, we simply use them! In other words, we ask these equations to talk about the position we are interested in: the collision point. And they express: |
|
|
 |
xe = 0,8 m/s² . te² |
[1] |
|
| vBe = 1,6 m/s² . te |
[2] |
|
| xe = 24 m – 0,7 m/s² . te² |
[3] |
|
| vNe = – 1,4 m/s² . te |
[4] |
|
|
|
These equations, on the other hand, are specific for the instant we are interested in. |
I knew it all along: we have fallen into a system with as many equations as unknown variables (4x4), in which these unknown variables are the answers to our exercise. If you have followed through the process so far, I´ll advise you to stop reading now, and try to solve this without any help, because what is left for us isn´t physics: it´s algebra; given that there are 7583 different ways to solve this, and only one way to learn it: practicing. |
|
|
Oh well, since you insist… after all, this is why No me salen exists. You equal the second terms of equations [1] and [3]
0,8 m/s² . te² = 24 m – 0,7 m/s² . te²
From there, we solve for te , and we are left with
te = 4 s
You replace this value in [1] and [3] |
 |
|
| and in [2] and [4] |
|
Este es el carnero negro (antes de la colisión, claro está). Si querés conocer al carnero blanco tendrás que resolver este mismo ejercicio desde una nueva perspectiva: abajo tenés la instrucción. |
|
|
|
|
And at last, the graphs. Notice how I set them up: in columns, always in the same order, and with a same time scale, some call this way “in tandem”. |
|
|
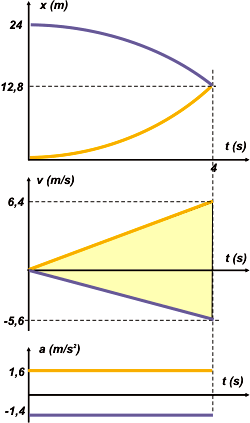 |
The curves are arched parabolas. A parabola with a positive concavity (smiley) represents a positive acceleration. A parabola with a negative concavity (sad) represents a negative acceleration. (A parabola without any concavity is not a parable, but a straight line. Ha, ha).
Take a look at the velocities graph; which ram is always moving with positive velocity? Which one has always negative velocities?
The black ram, from the moment he takes off until he crashes, increases his speed… but reduces his velocity. The shaded area shows an important fact… which one? How much are those areas? Does it mean anything that one of the areas is above the time axis, while the other one sits below it?
There are still other interesting details to consider with these graphs: go ahead, look for them… discuss what you know about this movement with them. |
|
|
 |
| Note: this same exercise is solved again, under different conditions: relative motion. You can find it here. |
|
| Challenge: The black ram takes off 1 second after the white one. (If you can´t nail it, you can see it in the exercise of the carafe and the water heater, here). |
|
| Some rights reserved. Reproduction allowe by quoting the source. Translated by Tomás de Udaetai. Last Updated jul-18. Buenos Aires, Argentina. |
|
|
| |
|