 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
| |
 |
FIS c7.04 - Dos carneros (uno blanco y otro negro) están en reposo, uno frente al otro, distanciados 24 m. En un instante dado, ambos parten para chocarse. Suponiendo que sus aceleraciones son constantes, y sus módulos 1,6 m/s² y 1,4 m/s² respectivamente. A partir de un
sistema de referencia en el cual el carnero blanco
está en reposo, determinando sus ecuaciones
horarias respecto al mismo. Trazar los gráficos
correspondientes. |
|
Te recomiendo fervientemente que antes de resolver este ejercicio te fijes cómo lo resolví desde un sistema de referencia fijo a la Tierra, acá: c3.42
La propuesta es rehacer el mismo problema pero con un SR montado en el lomo del carnero blanco. De modo que si él se mueve para allá o para acá, su posición va a ser cero, siempre cero, ¿se entiende? Si el tipo decide arrancar con todo y acelerar a fondo para atropellar al negro, él va a seguir estando en la posición cero, con velocidad cero y con aceleración cero... Y todo el universo se va a estar moviendo, y acelerando hacia atrás... ¡ni qué hablar de lo que le ocurre al carnero negro!
Pero no te asustes, todo tiene solución. El sistema móvil que permite movimientos adentro suyo es la imaginación del carnero blanco. Es el carnero blanco. De modo que serán: VNB, la velocidad del carnero Negro visto por el carnero Blanco. VBT, la velocidad del carnero Blanco visto desde la Tierra por un observador asustadísimo. Y VNT, la velocidad del carnero Negro visto por el mismo observador. Como siempre se cumple que
|
VNT = VNB + VBT
Pero qué pasa con las aceleraciones. Exactamente lo mismo. Si dividimos la igualdad anterior toda por el mismo intervalo de tiempo nos queda:
aNT = aNB + aBT
|
 |
|
|
Carnero: Ovis aries. Macho de la oveja; rumiante ungulado que nunca hace paro; de la familia de los bovidae. |
Visto desde la Tierra, las aceleraciones son las que se describían en el problema 3.12, o sea aNT = – 1,4 m/s² (acordate que habíamos puesto el sentido positivo de las x apuntando del blanco hacia el negro), y aBT = 1,6 m/s². Despejando
aNB = aNT – aBT
aNB = – 3 m/s²
O sea, para el carnero blanco, que se siente el centro del universo, el carnero negro retrocede hacia el centro, hacia él, con una aceleración de 3 m/s². ¡Era lo lógico!
¡Podría haberlo predicho sin saber jota de física! |
|
|
Armemos las ecuaciones del carnero negro (las del blanco son todas cero, cero, cero).
x = 24 m – 1,5 m/s² . t2
v = – 3 m/s² . t
Pedirles a estas ecuaciones que hablen del encuentro es lo mismo que pedirles que hablen de la posición cero, o sea del carnero blanco, centro del mundo.
0 m = 24 m – 1,5 m/s² . te2
ve = – 3 m/s² . te
Ya lo sabía... dos ecuaciones con dos incógnitas. ¡Es mucho más fácil este planteo que el original! (el original terminaba en un 4x4). De la primera ecuación:
te² = 24 m / 1,5 m/s²
|
|
|
| |
te = 4 s |
¡lo mismo que en el original! |
| |
|
Ahora con este resultado voy a la segunda ecuación y me queda...
ve = – 3 m/s² . 4 s
|
|
|
| |
ve = – 12 m/s |
¿lo mismo que en el original? |
|
|
|
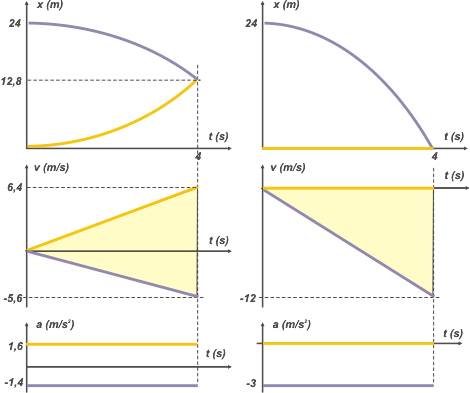
| Miremos cómo quedan los gráficos. Te voy a hacer dos columnas. A la izquierda los mismos gráficos que tenés en el problema 3.12, o sea, los carneritos vistos por el observador fijo a la Tierra. Y la columna de la derecha, el universo visto por el carnero blanco. |
|
|
 |
|
|
Si te ponés a contemplar los gráficos tenés muchas cosas para descubrir, áreas que son iguales, diferencias entre magnitudes que valen lo mismo, etc., etc. Inspirate. |
|
 |
| DESAFIO: el mismo que en el 3.12, o sea, que el carnero negro sale con toda la furia, pero 1 segundo después que el blanco. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
| | |
|
|

