 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento uniformemente variado)
|
|

|
| NMS c3.28 - Un calefón y una garrafa están en reposo, uno frente al otro, distanciados 24 m. En un instante dado, parte el calefón y 1 segundo después parte la garrafa, ambos para chocarse. Suponiendo que sus aceleraciones son constantes, y sus módulos 1,6 m/s² y 1,4 m/s² respectivamente, determinar en qué instante y en qué punto del camino se produce el encuentro, y qué velocidad tiene cada uno en ese instante. |
|
¡Otra vez el calefón y la garrafa! ¡No puede ser! ¡Pero qué artefactos más molestos!
No nos calentemos... hagamos el esquema. |
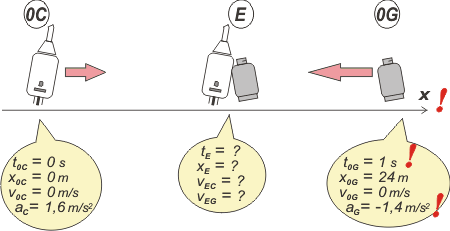 |
|
|
Mirá el signo de la aceleración de la garrafa: ¿cómo hubiera sido si el SR elegido tuviese sentido contrario? Y en ese caso, ¿cuánto hubiera valido la aceleración del calefón?
Tené a mano los modelos de las ecuaciones horarias de los MRUV, que estamos por usarlos. |
|
|
 |
x = xo + vo ( t – to ) + ½ a ( t – to )²
v= vo + a ( t – to ) |
|
|
Vamos a escribir las ecuaciones que describen el movimiento de ambos carneros. ¿Cuántas son? Dos para el blanco, dos para el negro, total cuatro. Para hallarlas basta con reemplazar las constantes de las ecuaciones generales (to, xo, vo y a) por las constantes iniciales de cada artefacto. |
|
|
| calefón |
x = 0,8 m/s² . t²
v = 1,6 m/s² . t |
|
Estas son las ecuaciones que describen TODO el fenómeno del movimiento que cuenta el enunciado. |
| garrafa |
x = 24 m – 0,7 m/s² . ( t – 1 s )²
v = – 1,4 m/s² . ( t – 1 s )
|
|
Y ahora, simplemente, ¡las usamos! Es decir, les pedimos a esas ecuaciones que hablen del punto de interés: el encuentro. Ellas dicen: |
|
|
 |
xE = 0,8 m/s² . tE² |
[1] |
|
| vEC = 1,6 m/s² . tE |
[2] |
|
| xE = 24 m – 0,7 m/s² . ( te – 1 s )² |
[3] |
|
| vEG = – 1,4 m/s² . ( tE – 1 s ) |
[4] |
|
|
|
Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan. |
Lo sospeché desde un principio: hemos caído en un sistema de tantas ecuaciones como incógnitas (4x4) en donde las incógnitas son las que pide el enunciado del problema. Si entendiste hasta aquí, el mejor consejo es suspender la lectura y tratar de resolverlo sin ayuda, ya que lo que queda no es física: es álgebra; ya que lo que queda tiene 7.583 modos diferentes de resolución, y uno sólo de aprenderlo: practicando.
¡Ah! Insistís... bueno, para eso está No me salen. Igualo los segundos miembros de [1] y [3]
0,8 m/s² . tE² = 24 m – 0,7 m/s² . ( tE – 1 s )²
0,8 m/s² . tE² = 24 m – 0,7 m/s² . ( tE² – 2tEs + 1 s²)
0,8 m/s² . tE² = 24 m – 0,7 m/s² . tE² + 1,4 m/s tE – 0,7 m
0 = 23,3 m + 1,4 m/s tE – 1,5 m/s² . tE²
Una cuadrática... ¡qué miedo! Calculo tE (hay dos resultados, pero uno de ellos es fácil de descartar). |
|
|
|
|
|
Reemplazo este valor en [1] y [3] y verifico que en ambas me da el mismo resultado:
xE = 0,8 m/s² . (4,55 s)²
xE = 24 m – 0,7 m/s² . ( 4,55 s – 1 s )²
|
|
|
| |
xE = 15,75 m |
|
(aproximado) |
|
|
|
| También voy a las ecuaciones [2] y [4]. |
|
|
| |
vEC = 7,1 m/s |
|
(aproximado) |
|
|
|
| |
vEG = – 4,8 m/s |
|
(aproximado) |
|
|
|
Por último los gráficos. Fijate cómo los hago: encolumnados, siempre en el mismo orden, y con una misma escala de tiempo; algunos llaman a esta manera "en tándem". |
|
|
|
|
 |
| |
|
| DESAFIO: Comparar estos gráficos con los de los carneros (3.42). |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente (me refiero a la reproducción de este material didáctico, no a la reproducción sexual de sus lectores, está claro). Última actualización ago-13. Buenos Aires, Argentina. |
|
|
| |
|

