home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC


  

manolito

No me salen c3.03 *- Un chico deja caer piedritas desde el balcón de su casa. El portero, que está en la vereda, observa que una de las piedras tarda 0,2 segundos en pasar frente a la puerta de entrada, que tiene 2 m de altura. Con esta información, hallar a qué altura del piso parten las piedras. (SUGERENCIA: tomar un sistema de referencia con origen en el borde superior de la puerta).

¿Qué tal si nos ponemos en transgresores y desechamos la sugerencia? (después te cuento por qué nos la hacen y por qué a mí me resulta atractiva la idea de desecharla).

Por supuesto, el primer e inevitable paso es hacer un esquema del problema.

  

Como siempre lo primero que hacemos es detectar los puntos o situaciones que aparecen en el problema y les ponemos nombre. 0 he llamado al punto inicial desde el que el chico deja caer las piedras. S al borde superior de la puerta, y P al borde inferior, en la vereda. De paso indico al vector g, que se vea bien que apunta en sentido contrario al del SR elegido.

Al lado de cada punto N nombrado se "descuelga" una "ventana automática":

tN = ...
yN = ...
vN = ...

Fijate bien qué puse en tP. ¿Se entiende por qué? Si el instante en que la piedra pasa por el borde superior de la puerta valiera 4,5 s, ¿cuánto valdría el instante en que llega al piso? Después voy a hacer otro comentario más sobre esto.
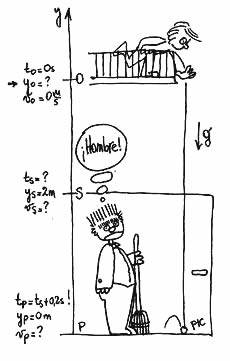
Ahora nos preguntamos... ¿Cuántas ecuaciones horarias describen este problema? Dos, pues se trata de un MRUV. ¿Tenés los "modelos" a mano? Yo sí.

y = yo + vo ( t – to ) + ½ g ( t – to )2

v = vo + g ( t – to )

  

Reemplazamos las constantes del movimiento (to, yo, vo y a) en los "modelos", y nos quedan:

  

y = yo – 5 m/s² . t2

v = – 10 m/s² . t

 Estas son las ecuaciones que describen TODO el fenómeno del movimiento narrado en el enunciado

Y ahora las usamos. Es decir, que hablen especialmente de los puntos S y P. En este caso, la segunda ecuación horaria, la de velocidad, no agregaría nada al problema ya que las velocidades vS y vP no son dato y el enunciado no pide averiguarlas (aunque podría). Entonces podemos no usarla y hacer más breve la cosa. Si no nos apiolamos de esto y la usamos, no hay drama.

La primera ecuación "habla" de los puntos S y P:

  
2 m = yo – 5 m/s² . tS² [1]
0 m = yo – 5 m/s² . ( tS + 0,2 s )² [2]
 

Tenía que ocurrir... hemos caído en un sistema de tantas ecuaciones como incógnitas (2x2), donde las incógnitas son yo y tS. (La primera es la altura que pregunta el enunciado). Pero si en lugar de escribir tS + 0,2 s hubiéramos escrito directamente lo que correspondía, es decir tP, ¡las incógnitas hubieran sido tres! Bueno, pero en ese caso hubiéramos agregado una tercera ecuación que dijera la obviedad:

tS + 0,2 s = tP

Sería entonces un sistema de 3x3.

El resto por supuesto es álgebra. La física del problema ya terminó y no fue tan difícil. Sí, en cambio, la matemática que nos falta es un poquito complicada... ¡pero no es física! La sugerencia que trae el enunciado es justamente para que las ecuaciones que queden tengan un álgebra de resolución más sencilla, pero al costo de establecer un SR rebuscado, antinatural (cosa que no nos asusta, al contrario, nos divierte), pero que a nadie se le ocurriría de entrada. Yo prefiero encarar los ejercicios siempre con la misma política, así todos los problemas se resuelven de la misma manera y sin tener que encontrar "trucos" ni "genialidades exóticas", sin planificar cambios estratégicos de SR a la mitad del problema. La física no debe ser sólo para genios o inspirados.

Acá te muestro una resolución algebraica posible. Primero desarrollo el cuadrado del binomio de [2].

 

0 m = yo – 5 m/s² . ( tS² + tS . 0,4 s + 0,04 s²)

  
Distribuyo el factor 5 m/s² con el paréntesis largo. Queda así:  

0 m = yo – 5 m/s² . tS² – 2 m/s . tS – 0,2 m                                [3]

  
Ahora resto miembro a miembro la [1] con la [3]. Mirá lo que queda.  

2 m = 2 m/s. tS + 0,2 m

 
De ahí despejo tS y lo calculo. Me da tS = 0,9 s  
Con este valor voy a las ecuaciones [1] y [2] para verificar que en las dos da lo mismo, y efectivamente  
  yo = 6,05 m        
Moraleja: no subestimar a los porteros.  
DESAFIO: Hallar las velocidades con que pasa por el borde superior de la puerta y con que llega al piso. Plantear (sólo plantear) el problema con otro SR cualquiera.  

*Este problema pertenecía a la guía de problemas de la materia Fisica, que se usó hasta el año 2002. Se trataba del ejercicio 3.23.

  
  Ricardo Cabrera
Prohibida la reproducción total o parcial de este material didáctico de primerísima calidad por cualquier medio visual, gráfico, sonoro u holográfico con fines comerciales. Las transgresiones a esta disposición serán penalizadas con 27 años de reclusión en la Antártida y trabajos forzosos. Última actualización ago-06. Buenos Aires, Argentina.