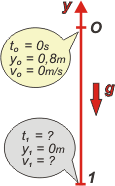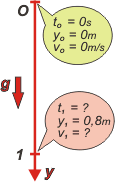NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
No me salen c3.02* - A Jaimito se le escapa la botella de cerveza que tiene en la mano, a 80 cm sobre el piso. ¿Qué velocidad tendría la botella al llegar al piso? ¿Cuánto tiempo tiene Jaimito para alcanzarla? |
|
 |
| Vamos a hacer una resolución doble. En el sector izquierdo, el problema visto desde un SR que apunta hacia arriba con el cero en el piso (este sería el más natural, pues los datos referidos en el enunciado lo adoptan tácitamente). En el sector derecho, con un SR positivo hacia abajo y el cero en la mano de Jaimito (¡"Jaimito"! ¡Qué antigüedad!). Veremos que es lo mismo usar cualquier SR. Lo importante es prestar atención a los esquemas... el valor de las constantes iniciales, de las velocidades, de las aceleraciones. |
|
|
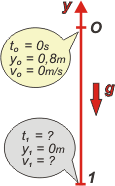 |
Ahora, como siempre, escribimos las ecuaciones horarias del móvil; para ello tenemos que tener a mano los "modelos" de ecuación horaria del movimiento en cuestión.
y = yo + vo ( t – to ) + ½ g ( t – to )2
v = v o + g ( t – to )
|
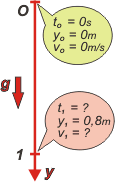 |
|
|
|
| Vertical hacia arriba |
|
|
|
Vertical hacia abajo |
Y en ellas reemplazamos las constantes
(to, yo, vo y a) por las constantes "iniciales" (en este caso está de más el entrecomillado) de nuestro movimiento. Esas constantes las encontrás en el globito amarillo. Observemos atentamente las diferencias. |
|
|
|
Y en ellas reemplazamos las constantes
(to, yo, vo y a) por las constantes "iniciales" (en este caso está de más el entrecomillado) de nuestro movimiento. Esas constantes las encontrás en el globito verde. Observemos atentamente las diferencias. |
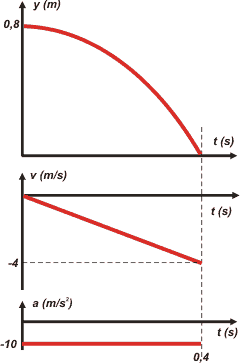
y = 0,8 m – 5 m/s² . t2
v = – 10 m/s² . t |
|
|
|
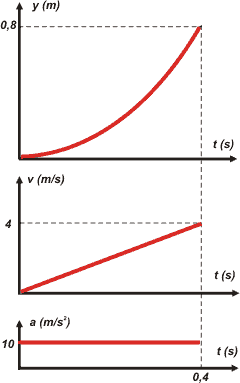
y = 5 m/s² . t2
v = 10 m/s² . t |
| Ahora las usamos a cada una de ellas para que hablen (las especializamos, como dirían los físicos) del punto de interés (el otro que no es el inicial). Ellas dicen: |
|
|
|
Ahora las usamos a cada una de ellas para que hablen (las especializamos, como dirían los físicos) del punto de interés (el otro que no es el inicial). Ellas dicen: |
0 m = 0,8 m – 5 m/s² . t12
v1 = – 10 m/s² . t1 |
|
|
|
0,8 m = 5 m/s² . t12
v1 = 10 m/s² . t1 |
Quedó un sistema de tantas ecuaciones como incógnitas, donde las incógnitas son las que pide el enunciado del problema. Aquí terminó, entonces, la física del problema, y el resto es álgebra. Vamos a resolverlo.
De la primera: |
|
|
|
Quedó un sistema de tantas ecuaciones como incógnitas, donde las incógnitas son las que pide el enunciado del problema. Aquí terminó, entonces, la física del problema, y el resto es álgebra. Vamos a resolverlo.
De la primera: |
|
|
|
|
|
| Como to = 0, este es el tiempo que tiene Jaime para evitar que la botella se haga bolsa contra el piso. Con este valor de t1 vamos a la segunda ecuación, y |
|
|
|
Como to = 0, este es el tiempo que tiene Jaime para evitar que la botella se haga bolsa contra el piso. Con este valor de t1 vamos a la segunda ecuación, y |
|
|
|
|
|
 |
|
|
|
 |
|
|
|
| |
| Estas son las ecuaciones que describen TODO el movimiento. |
| |
Usar o (como dicen los físicos) especializar una ecuación horaria significa reemplazar las variables:
x y t. |
| |
| |
| |
| |
| Los gráficos los hacemos SIEMPRE en tándem. |
| Te habrás dado cuenta de que el valor de g no fue el mismo. Para el sistema que apunta hacia arriba fue g = – 10 m/s², y para el sistema que apunta hacia abajo fue g = + 10 m/s²; como ves... NO DEPENDE DE LO QUE HAGA EL MOVIL, en este caso la botella: siempre caía. El signo de g sólo depende del SR. |
|
|
| |
|
|
| DESAFIO: Rehacer el problema pero tomando como instante de tiempo inicial el valor to= 5 s. |
|
|
| *Este problema pertenecía a la guía de problemas de la materia Fisica, que se usó hasta el año 2002. Se trataba del ejercicio 3.20. |
|
|
 |
| |
|
| Prohibida la reproducción total o parcial de este material didáctico de primerísima calidad por cualquier medio visual, gráfico, sonoro o tridimensional. Las transgresiones a esta disposición serán penalizadas con 25 años de reclusión en la Antártida y trabajos forzosos.
Sólo se permite su reproducción citando la fuente. Algunos otros derechos reservados. Agradezco a la atenta Geraldine Lagger por descubrir una errata y avisarme para que la corrija. Última actualización ago-06. Buenos Aires, Argentina. |
|
|
|