 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
No me salen c3.01*- Un trineo parte del reposo por una rampa inclinada, con aceleración constante. Pasa por un primer puesto de control con una velocidad de 5 m/s, y por el segundo puesto con una velocidad de 15 m/s. Si ambos puestos están distanciados 60 m, calcular la aceleración que experimenta, la distancia del punto de partida al primer puesto y el tiempo transcurrido desde que partió hasta que pasó por el segundo puesto.
Ningún otro modo de empezar un problema es tan útil como un buen y completo esquema. Nos permite contrastar la interpretación que hacemos de un enunciado con el enunciado mismo; nombrar datos e incógnitas, ordenarlos; establecer el sistema de referencia (SR); gozar de la vida; etc.
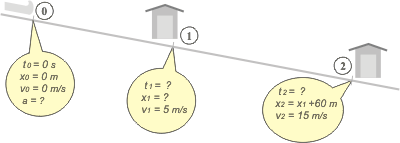
Nos damos cuenta de que en el problema hay tres situaciones importantes: la partida, que llamamos 0, el primer puesto 1, y el segundo puesto 2. Volcamos valores y definimos el SR más económico. De lo que resulta:
|
|
|
|
Dos ecuaciones horarias describen el movimiento del trineo: la de posición y la de velocidad (como todo MRUV). Los "modelos" ya te los sabés de memoria... pero una vez más: |
|
|
x = xo + vo ( t – to ) + ½ a ( t – to )2
v = vo + a ( t – to )
|
|
|
| Para hallar las ecuaciones del trineo en particular basta con que reemplacemos las constantes de los modelos (to, xo, vo y a) por los datos de la partida que en este caso también los hemos llamado "0". |
|
|
x = ½ a t 2
v = a . t
|
|
Estas son las ecuaciones que describen TODO el movimiento |
| Quedaron así, súper cortitas, y simpáticas. Ahora... ¡las usamos! Es decir, les pedimos a esas ecuaciones que en vez de hablar de todas las infinitas posiciones, velocidades e instantes de tiempo por los que pasa el trineo, hablen tan sólo de aquellos puntos que para nosotros tienen interés: el 1 y el 2, que son justamente los indicados en el esquema. |
|
|
 |
x1 = ½ a t1² |
|
[1] |
| 5 m/s = a t1 |
|
[2] |
| x1 + 60 m = ½ a t2² |
|
[3] |
| 15 m/s = a t2 |
|
[4] |
|
|
|
| Ahora sí. Tenemos un sistema de cuatro ecuaciones con cuatro incógnitas (¡qué miedo que me da!). Lo importante es comprobar lo fácil que se resuelven los problemas de cinemática con las ecuaciones horarias. Acá terminó la física del problema. El resto es álgebra, y tal vez sea menos dramático. Hay 258.347 formas diferentes de resolver el sistema, y una sola manera de aprender a resolverlo: practicando sin ayuda. De todos modos... de [2] |
|
 |
| |
t1 = ( 5 m/s) / a |
|
[5] |
| de [4] |
|
|
|
| |
t2 = ( 15 m/s) / a |
|
[6] |
| Ahora reemplazo la [1] en la [3] |
|
|
| |
½ a t1² + 60 m = ½ a t2² |
|
[7] |
|
|
|
y en la [7] reemplazo la [5] y la [6], entonces queda una única ecuación con una única incógnita que es a. La despejo y calculo: |
|
|
| |
½ a (5 m/s)² |
+ 60 m |
= |
½ a (15 m/s)² |
|
|
|
| a² |
a² |
|
|
|
| 60 m = |
|
½ 225 (m/s)² |
– |
½ 25 (m/s)² |
|
|
|
| a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
| ¿Pudiste seguirme? El resto es fácil. Con ese valor de aceleración voy a las ecuaciones de arriba... |
|
|
|
|
|
|
|
|
| |
t2 = 9 s |
 |
| |
|
| |
t2 – t1 = 6 s |
| |
|
| |
x2 = 67,5 m |
|
|
|
| Ahora los gráficos |
|
|
 |
¿A que no te animás a decirme cuánto vale el área que te marqué en amarillo, sin hacer cuentas? Bueno, si no te animás... hacelo igual. |
DESAFIO: Muchos temerosos resuelven este problema tomando los datos iniciales (to, xo, vo) en el primer puesto de control, así:
to = 0 s, xo = 0 m y vo = 5 m/s
Rehacelo con ese criterio. La enseñanza es que: siempre hay un SR para el cual el trabajo algebraico es mínimo. Claro, para acertarle a ese SR hay que tener experiencia. |
| *Este problema pertenecía a la guía de problemas de la materia Física, que se usó hasta el año 2002. Se trataba del ejercicio 3.6 |
|
| |
|
|
|
| Desafío: rehacer el ejercicio pero eligiendo el cero de las posiciones y de los tiempos por el paso por delante del puesto 1. |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Queda claro que no se trata de que llames a la fuente por teléfono y le digas que se encuentran en 9 de Julio y Córdoba a las 3 de la tarde. Es cierto, en esa esquina hay una fuente... pero... cómo lo explico... Última actualización ago-06. Buenos Aires, Argentina. |
|
| |
|
|
|
|
|
| |
|
| |
|
| |
|

