CINEMATICA, No me salen 09, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)

NMS c2.08*-. Dos corredores pedestres juegan una carrera de ida y vuelta por la misma pista recta de 150 metros de largo. Ambos parten simultáneamente y corren a velocidad constante; el más rápido a 6 m/s y el otro a 5 m/s. Hallar en qué instante y posición se encuentran.

Este problema se tomó en un primer examen parcial en la sede Paseo Colón (QEPD), y resultó una verdadera masacre (QEPDn). Lo resolvió correctamente el 5% de los estudiantes, y chapuceramente otro 10%. El 85% restante levantó tanta presión que cuando se supo quién había sido el autor del problema temí por mi integridad física.

En un acto de arrojo y valentía expliqué la resolución del problema el día que repartíamos las notas. No fue muy diferente de lo que te voy a contar ahora:

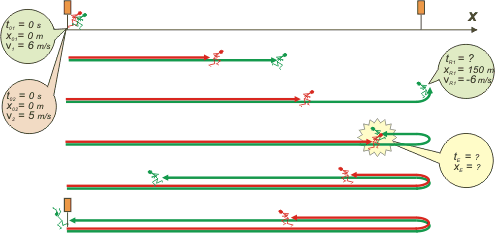
Lo primero fue hacer un esquema, como siempre. Claro que, así como a ellos se los fui contando a medida que lo hacía en el pizarrón, a vos te lo voy a hacer en varios pasos... de arriba hacia abajo, a medida que avanza el tiempo de la carrera.

cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia

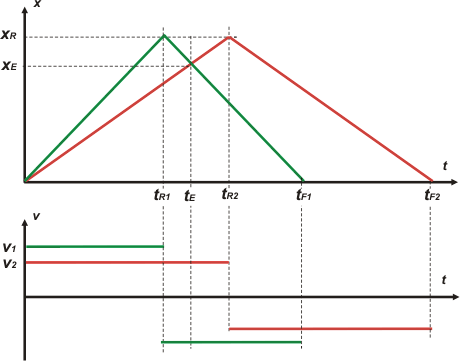
El corredor más veloz es el verde y el otro, el rojo. Parten simultáneamente desde la largada. Como ves, a medida que avanza la carrera el verde le saca más ventaja al rojo. Se encuentran (se cruzan) cuando el verde ya está de vuelta y el rojo todavía va de ida. A esta altura de la explicación los pibes me miraban como diciendo "la verdad, hasta acá, es una pavada atómica". Yo ya me sentía más confiado y pensaba que ya había salvado el pellejo... entonces me animé, y les propuse hacer el gráfico antes de resolver el problema. En el pizarrón usé colores, como acá.

Tanto en el caso del gráfico como en el del esquema remarqué lo útiles que eran para ponerle nombre a las cosas, a los datos o incógnitas cinemáticas de las que teníamos que ocuparnos. Por ejemplo el instante y la posición de encuentro, que llamé t_E y x_E, respectivamente; o los instantes en que cada corredor pegaba la vuelta, que llamé t_R1 y t_R2 (la R por retorno), y la posición en que ello ocurría, x_R, ídem. Recién entonces, y con mucha parsimonia, empecé a escribir las ecuaciones que describían la carrera. Son cuatro, dos para cada corredor, y todas se construyen con el mismo modelo: x = x_o + v ( t – t_o )

1, ida		*x = 6 m/s t*
2, ida		*x = 5 m/s t*
1, vuelta		*x = 150 m – 6 m/s ( t – t_R1 )*
2, vuelta		*x = 150 m – 5 m/s ( t – t_R2)*

Luego le pedí a esas ecuaciones que hablaran de los eventos que nos pudieran interesar. La segunda y la tercera hablarían del encuentro, lógicamente. La primera del instante en que el verde pega la vuelta y la cuarta no podía decirnos nada que nos interesara... pobrecita.

[1]	*150 m = 6 m/s . t_R1*	1, ida, en *t_R1*
[2]	x_E = 5 m/s . t_E	2, ida, en t_E
[3]	x_E = 150 m – 6 m/s ( t_E – t_R1 )	1, vuelta, en t_E

Supongo que ya se imaginan la cara que pusieron los chicos cuando contamos la cantidad de ecuaciones e incógnitas, un momento antes de que dibujara la llave que indica que se había acabado la física y que el resto era álgebra. Igual se los resolví.

Despejo t_R1 de la [1] y lo que me da, 25 s, lo meto en la [3]. De esta ecuación igualo su segundo miembro al segundo miembro de la [2]

5 m/s . t_E = 150 m – 6 m/s ( t_E – 25 s )

5 m/s . t_E = 150 m – 6 m/s. t_E + 150 m

5 m/s . t_E + 6 m/s. t_E = 300 m

11 m/s . t_E = 300 m

t_E = 350 m / 11 m/s.

t_E = 27,27 s.

con esto voy a cualquiera de las dos ecuaciones que hablan del encuentro

x_E = 136,35 m

NOTA: Después de resolver juntos el ejercicio nos quedamos charlando como media hora sobre cuáles podrían haber sido los motivos por los que este problema, que ahora parecía tan sencillo, había sido un karma el día del examen. ¿A vos qué te parece?

*Ejercicio tomado en el primer parcial de Física del año 1994 en la sede Paseo Colón del CBC (actualmente Montes de Oca).

Desafío: mirá el gráfico de posiciónes en funcion del tiempo. ¿Qué representa el segmento vertical (línea de puntos) que va desde t_R2 hasta la intersección con la recta verde?