NO ME SALEN
SOLVED PHYSICS EXCERCISES FROM THE CBC
(Uniform movement)
|
|

|
Aditional No me salen 2.8* -. Two pedestrian runners are racing each other in a round trip by the same track, a 150m long track. both of them start at the same time and run with constant speed; the fastest one at 6m/s and the other one at 5m/s.
|
This problem was in the first midterm exam in the Paseo Colón campus university (R.I.P), it was a real massacre (R.I.P´em). A 5% of the students solved it correctly, and a 10% solved it kinda poorly. The remaining 85% raised so much pressure that when they found out who was the author of this problem, I feared for my physical integrity.
In an act of spunk and courage I explained how to solve this problem the same day I handed out the grades. It wasn´t as different as what I am going to explain to you now:
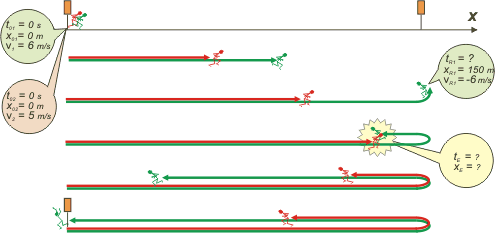
The first thing is making a scheme, as usuall. Obviously, as I was explaining this, I was drawing in the board, so we are going to do the same by segments... from top to bottom, accordingly as the race passes. |
|
|
|
| cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia |
|
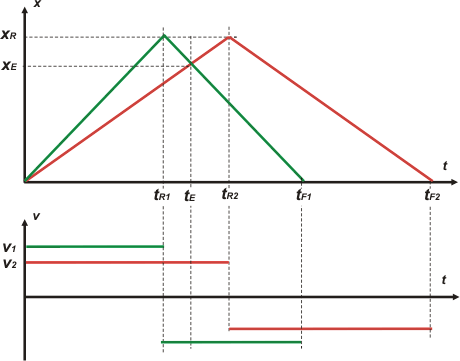
The fastest runner is the green one, the other is the red one. They start running at the same time at the starting point. As you can see, while the green one runs, he leaves the red one behind. They find each other (cross) when the green one is returning and the red one is till going. At this point of the explanation, the laddies were looking at me, saying: ``truly, up to this point, it´s stupidly easy´´. I was feeling more confident by then, thinking I saved my neck... so I bucked up, and asked them to do the graphic before solving the problem. In the board I used some colors, as I am doing right now. |
|
|
|
| In the graph and in the scheme, I highlighted how usefull these were to name things, information, unknown kinematics wich we had to take care of. For example, the instant and meeting poing, wich I called tE and xE, respectively; or the instants instantes when each runner started coming back, wich I called: instants tR1 and tR2 (R for return), and the position according to that time, xR , ditto. And just then, with a lot of parsimony, I started writing the equations that describe the race. They are four, two for each runner, and every one of them are built with the same model: x = xo + v ( t – to ) |
|
| 1, going |
|
x = 6 m/s t |
|
| 2, going |
|
x = 5 m/s t |
|
| 1, coming |
|
x = 150 m – 6 m/s ( t – tR1 ) |
|
| 2, coming |
|
x = 150 m – 5 m/s ( t – tR2 ) |
|
|
|
| Then, I asked those equations to talk about the events that could pick our interest. The second and the third one would talk about the encounter, logically. The first about the instant where the green runner starts cming back, and the forth one couldn´t tell us nothing interesting... poor thing. |
|
| [1] |
 |
150 m = 6 m/s . tR1 |
1, going, in tR1 |
| [2] |
xE = 5 m/s . tE |
2, going, in tE |
| [3] |
xE = 150 m – 6 m/s ( tE – tR1 ) |
1, coming, in tE |
|
|
I think you can already picture the kids´ faces when we counted the ammount of equations and unknowns an instant before drawing the "{" , indicating that the physics part was over and there was just algebra to be done. I solved it for them anyway.
I find tR1 using [1] and the result, 25 s, can be used in [3]. From this equation, I equal it´s second member to the second member of [2]
5 m/s . tE = 150 m – 6 m/s ( tE – 25 s )
5 m/s . tE = 150 m – 6 m/s. tE + 150 m
5 m/s . tE + 6 m/s. tE = 300 m
11 m/s . tE = 300 m
tE = 350 m / 11 m/s.
|
|
|
|
| I can use this in the encounter equations and... |
|
|
|
|
|
| NOTE: after solving together the excercise, we spend like half an hour talking about the reasons this so seemingly (now) easy excercise, was such a karma in the exam. What do you think? |
|
| |
 |
| |
*Excercise copied from the first physics exam in 1994, in the Paseo Colón CBC. |
|
| Challenge: look at the position-time graph. What does the vertical line of points (the one that goes from tR2 to the intersection with the green straight line) represents? |
|
| Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Those ones not obeying these rules will be sentenced to hard labor in the Antarctica. Translated by Santi Pisci. Last updated ago-15. Buenos Aires, Argentina. |
|
|
|

