 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
 |
NMS c2.07 - Andrés va en su bicicleta, con velocidad constante de 14 km/h, en una calle rectilínea siguiendo a Karina, que va corriendo en el mismo sentido, a 5 km/h, también con velocidad constante.
Si inicialmente estaban distanciados 100 m, hallar cuánto tiempo después la alcanzará, y qué distancia avanzó cada uno. Trazar los gráficos posición-tiempo y velocidad-tiempo. |
|
¿Por dónde vamos a empezar sino por un esquema bien hecho?
|
| |
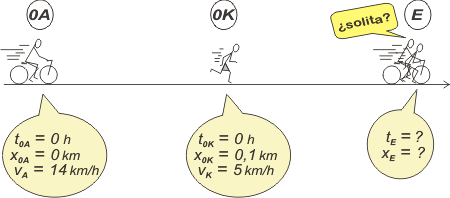 |
|
|
¿Cuántas ecuaciones horarias describen este problema? Dos, ya que hay dos móviles. Ambas surgen del mismo modelo ya que ambos se mueven uniformemente. El modelo es:
x = xo + v ( t – to )
Y, por lo tanto, reemplazo las constantes del modelo (azules) mirando las constantes elegidas en el esquema, de modo que las ecuaciones de este problema son: |
|
|
| |
la de Andrés
la de Karina |
x = 14 km/h . t
x = 0,1 km + 5 km/h . t |
|
Estas son las ecuaciones que describen TODO el movimiento descripto en el enunciado. |
| Ahora, ellas solitas resuelven el problema. Pidámosles que en lugar de hablar de las infinitas posiciones y sus respectivos instantes de tiempo por los que pasan Andrés y Karina, se refieran exclusivamente a la posición e instante de encuentro. (Ahora es cuando reemplazo las variables, las rojas). Entonces dicen: |
|
|
| |
 |
xe = 14 km/h . te
xe = 0,1 km + 5 km/h . te |
|
|
¡Listo! Encontramos un sistema de tantas ecuaciones como incógnitas (2x2); acá terminó la física. Lo que resta es álgebra. (Las ecuaciones son unas genias). Para resolver el sistema hay varios métodos: sustitución, igualación, sumas y restas, determinantes, y (el más saludable) chapuceo algebraico generalizado. Acá va uno... ¿cuál es?
14 km/h . te = 0,1 km + 5 km/h . te
te = 0,1 km / 9 km/h
te = 0,011 h
Entonces. como parten del instante 0 h, lo que tardan en encontrarse es:
Δte = 0,011 h – 0 h
|
|
|
|
|
|
Reemplazando te en cualquiera de las dos ecuaciones (mejor en las dos)... Y obtenemos:
xe = 0,156 km
Entonces: |
|
|
|
|
|
|
|
|
Los gráficos. Porsupu: Andrés en celeste y Karina rosa (eso es importantísimo). |
|
|
| |
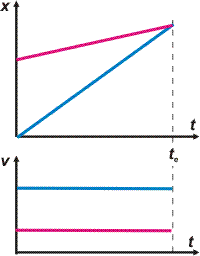 |
¿Te animás a ponerle a estos gráficos los datos que les faltan? ¿Te animás a calcular las áreas encerradas bajo las curvas x-t? ¿Te animarías a rehacerlos en escala y verificar los resultados gráficamente?
Tenés una vuelta más de tuerca de este ejercicio acá. Te lo recomiendo, te va a sorprender. |
|
|
 |
DESAFIO: Resolver el problema pero con un SR de sentido opuesto, por ejemplo uno en el que Andrés esté en x0A = 100 m y Karina en x0K = 0 m. Y para terminar (aunque esto pertenece a "Cuántica II"), averiguar qué contestó Karina.
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Este material es absolutamente gratuito; el mejor pago para el trabajo que me tomé es que aceptes del DESAFIO y lo resuelvas. Agradezco a Andrés Ciliberti que detectó una errata en este ejercicio. Última actualización abr-07. Buenos Aires, Argentina. |
|
|
| |
|

