 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
NMS c2.15- Andrés va de nuevo en su bicicleta, con velocidad constante de 14 km/h, en una calle rectilínea siguiendo a Karina, que va corriendo en el mismo sentido, a 5 km/h, también con velocidad constante.
Si inicialmente estaban distanciados 100 m, hallar cuánto tiempo después la alcanzará, y qué distancia avanzó cada uno. Resolver el ejercicio tomando como posición inicial en instante de Andrés 0,5 km y 2 h. |
|
¡Este ejercicio ya lo hicimos! Sí... me acuerdo... creo que es el 2.7. Sí, exactamente el mismo, pero ahora nos imponen una condición: que los resolvamos tomando como posición e instante inicial de Andrés unos valores absurdos. Me lo van a recontracomplicar... en fin... Acá va el nuevo esquema:
|
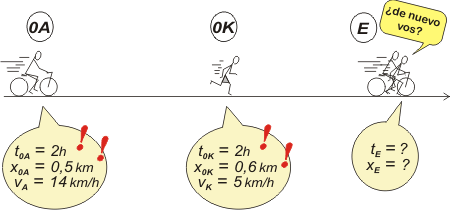 |
|
|
¿Cuántas ecuaciones horarias describen este problema? Dos, ya que hay dos móviles. Ambas surgen del mismo modelo ya que ambos se mueven uniformemente. El modelo es:
x = xo + v ( t – to )
Y, por lo tanto, reemplazo las constantes del modelo (azules) mirando las constantes elegidas en el esquema, de modo que las ecuaciones de este problema son: |
|
|
| |
la de Andrés
la de Karina |
x = 0,5 km + 14 km/h . ( t – 2 h )
x = 0,6 km + 5 km/h . ( t – 2 h ) |
|
Estas son las ecuaciones que describen TODO el movimiento descripto en el enunciado. |
| Ahora, ellas solitas resuelven el problema. Pidámosles que en lugar de hablar de las infinitas posiciones y sus respectivos instantes de tiempo por los que pasan Andrés y Karina, se refieran exclusivamente a la posición e instante de encuentro. (Ahora es cuando reemplazo las variables, las rojas). Entonces dicen: |
|
|
| |
 |
xe = 0,5 km + 14 km/h . ( te – 2 h )
xe = 0,6 km + 5 km/h . ( te – 2 h ) |
|
|
¡Listo! Encontramos un sistema de tantas ecuaciones como incógnitas (2x2); acá terminó la física. Lo que resta es álgebra. (Las ecuaciones son unas genias). Para resolver el sistema hay varios métodos: sustitución, igualación, sumas y restas, determinantes, y (el más saludable) chapuceo algebraico generalizado. Acá va uno... ¿cuál es?
0,5 km + 14 km/h . ( te – 2 h ) = 0,6 km + 5 km/h . ( te – 2 h )
9 km/h . ( te – 2 h ) = 0,1 km
te – 2 h = 0,1 km / 9 km/h
te = 0,011 h + 2 h
te = 2,011 h
Como arracaron en el instante 2 h, tardaron en encontrarse: |
|
|
|
|
|
Lo mismo que antes. Ahora reemplazando ese valor en cualquiera de las dos ecuaciones (mejor en las dos)... obtenemos:
xe = 0,656 km
Entonces: |
|
|
|
|
|
|
|
|
Como ves, los resultados que encontramos con el ejercicio original son exactamente los mismos que con el nuevo sistema de referencia estrambótico. Y la complejidad algebraica aumentó... cuánto... una pendejésima. ¡Por poco me desmayo! |
|
|
DESAFIO: Hacé los nuevos gráficos. |
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-07. Buenos Aires, Argentina. |
|
|
| |
|

