 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)

|
|

|
| |
 |
FIS c7.05- El maquinista de un tren que avanza con
una velocidad v1 advierte delante de él, a una
distancia d, la cola de un tren de carga que se
mueve en su mismo sentido, con una velocidad
v2 constante, menor que la suya.
Frena entonces, con aceleración constante.
Determinar el mínimo valor del módulo de dicha
aceleración, para evitar el choque.
SUGERENCIA: Adoptar un sistema de referencia
fijo a uno de los trenes. |
|
Ok, ok, non è facile... pero ya resolviste (supongo) algo muy pero muy parecido: el problema 2.8 de MRU. Tengo un plan, ya te lo cuento... Primero hacemos, como siempre, un esquema; y lo discutimos bien para estar seguros de que entendimos el ejercicio. Segundo, lo resolvemos como lo hubiéramos hecho antes de aprender Movimiento Relativo. Tercero, lo resolvemos desde el punto de vista del movimiento relativo tal como nos sugiere el enunciado, ¿dale?
Si hacemos esto vas a poder apreciar la potencia del "pensamiento relativo" y, tal vez, entiendas más adelante cuán importante resultó en la historia del conocimiento humano. Manos a la obra.
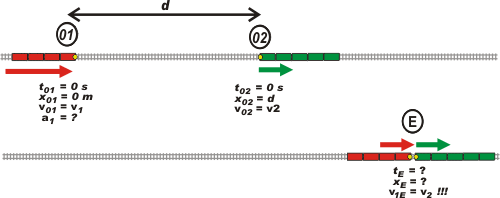
Se trata de un problema de encuentro, común y silvestre. El tren de pasajeros que viene atrás (rojo), a una velocidad v1, va rápido, como todos los trenes de pasajeros (?). El de adelante (verde) es de carga y va lento como todos los trenes de carga, a una velocidad v2. El maquinista del tren rojo (que está en el puntito amarillo) ve la cola del de carga (otro puntito amarillo) y luego de hacer un rápido cálculo dice: "¡a menos que reduzca mi velocidad uniformemente con cierta aceleración, me estrolo con el lerdo ese de adelante, y la repu@#&%!" e inmediatamente aplica los frenos.
No es fácil frenar un tren... pero no necesita frenarse totalmente para evitar el choque... le alcanza con llegar justito a casi tocarlo, con la misma velocidad con la que va el de adelante. Mirá en detalle el esquema. |
|
¿Te cierra? Ok, lo voy a hacer rápido porque es tema viejo. Escribo las ecuaciones de los dos trenes.
tren rojo posición → x = v1 . t + ½ a1 . t2
tren rojo velocidad → v = v1 + a1 . t
tren verde posición → x = d + v2 . t
ahora les pido a las tres ecuaciones que hablen del encuentro, el punto E |
|
|
 |
xE = v1 . tE + ½ a1 . tE² |
[1] |
| v2 = v1 + a1 . tE |
[2] |
| xE = d + v2 . tE |
[3] |
|
|
|
de [2] despejo a1
a1 = ( v2— v1 ) / tE [4]
eso lo meto en la [1] y la igualo con la [3]
v1 . tE + ½ ( v2 — v1) . tE = d + v2 . tE
distribuyo los factores de segundo término del primer miembro:
v1 . tE + ½ v2 tE — ½ v1 tE — v2 tE = d
saco factor común tE
tE ( v1 + ½ v2 — ½ v1 — v2 ) = d
resuelvo el paréntesis y despejo tE
tE = — 2 d / ( v2 — v1 )
meto eso en la [4] |
|
|
| |
a1 = — ( v2 — v1 )2 / 2 d |
este es el cálculo del maquinista |
|
|
|
Pongamos un ejemplo numérico: el de carga va a 2 m/s y el de pasajeros, que viene atrás, a 8 m/s. Lo alcanza a ver cuando lo tiene a 180 m. La aceleración deberá ser... a = — 0,1 m/s², de frenado, por supuesto.
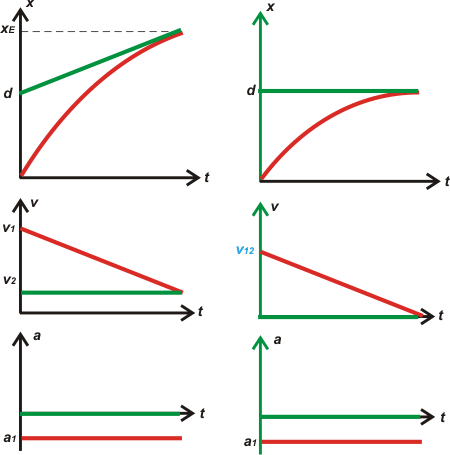
Habrás visto que no es un problema sencillo... pero tampoco imposible. Abajo te hice los gráficos. La columna de la izquierda describe el problema tal como te lo acabo de resolver hasta aquí. Y en la columna de la derecha, como lo vamos a resolver ahora, desde el punto de vista relativo.
El maquinista ve el tren de pasajeros y lo que encuentra es que se le está acercando peligrosamente. La velocidad con que se le acerca ¿cuál es? Sin hacer demasiado cálculo responde: ¡6 m/s, que no es otra que |v2— v1|! Este sencillo cálculo no es más que suponer que el de adelante está quieto, o si preferís, que el de adelante lleva atornillado un sistema de referencia móvil que se mueve junto con él a una velocidad v2, que en nuestro ejemplo numérico es 2 m/s. Si aplicamos la ecuación de Galileo
V1T = V12 + V2T
Velocidad del tren 1 visto desde Tierra es igual a la velocidad del tren 1 visto desde el 2, más la velocidad del tren 2 visto desde la Tierra
8 m/s = 6 m/s + 2 m/s
Cálculo inmediato y espontáneo que hizo el maquinista. Ahora enfrenta un problema de cinemática mucho más fácil que el anterior, ya que el tren de adelante, desde su propio sistema de referencia, está quieto a una distancia d. No necesita ecuación. Y la velocidad final del maquinista debe ser cero (cero para el nuevo sistema de referencia).
tren rojo posición → x = V12 . t + ½ a1 . t2
tren rojo velocidad → v = V12 + a1 . t
que hablen del encuentro |
|
 |
 |
d = V12 . tE + ½ a1 . tE² |
[1'] |
| 0 m/s = V12 + a1 . tE |
[2'] |
|
|
|
de [2'] despejo a1
a1 = — V12 / tE [3']
eso lo meto en la [1']
d = V12 . tE — ½ V12 . tE = ½ V12 . tE
mirá lo que queda
tE = 2d / V12
meto eso en la [3'], y... ¡sorpresa! |
|
|
| |
a1 = — V122 / 2 d |
este es el cálculo del maquinista relativo |
|
|
|
| Acordate: los gráficos de la izquierda son los clásicos y los de la derecha, los del movimiento relativo. |
|
|
 |
|
|
DESAFIO: Hallá todos los datos que faltan calcular sobre la base del ejemplo numérico que te di: 180 m, etc. Verificá que en los dos sistemas obtengas los mismos resultados, aceleración, tiempo de encuentro, distancias recorridas por los dos trenes, etc. Y por último... chan, chan, chan, chan... mirá las áreas en los gráficos v/t. |
|
 |
Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste?, mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente, o sea, a papá. Agradezco a Brisa Sánchez por la indicación de una errata. Última actualización set-06. Buenos Aires, Argentina.
|
|
| |
|

