NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
 |
Fc2.07 - Una cuadrilla de empleados del ferrocarril
viaja en una zorra por una vía rectilínea. En un
instante dado, por la misma vía y a 180 m por detrás,
ven venir un tren que viaja con una velocidad
constante de 36 km/h. ¿A qué velocidad mínima
y constante deberá moverse la zorra para
poder llegar a un desvío, que en ese instante está
120 m más adelante, para evitar el choque? |
|
Graficar velocidad y posición en función del
tiempo, para ambos móviles.
Resolver ahora, considerando que se requieren
10 segundos para accionar el cambio de vías.
Como siempre, hay que empezar con un esquema. Si no lo hacés, perdés. Si lo hacés mal o incompleto, perdés. |
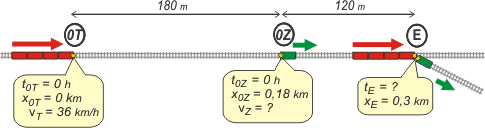
| |
paso 1 |
¿Te gusta éste? Del tren tomé el punto delantero y de la zorra, el trasero (perdón); y te los marqué con un punto amarillo. No parece tan difícil, ¿no? Y te soluciona la vida. Mirá qué fácil que es el problema ahora. Tenete el modelo de ecuación horaria cerca. Acá está.
x = xo + v ( t – to )
Reemplazá las constantes de cada móvil por las constantes en la ecuación. Las de la ecuación son éstas, las que te puse en rojo
x = xo + v ( t – to )
y las de los móviles las encontrás al lado de cada móvil en el comienzo del movimiento. Las ecuaciones quedan así:
Para el tren → x = 36 km/h . t
Para la zorra → x = 0,18 km + vZ . t
ahora les pedimos a ambas que hablen de los puntos que resulten interesantes. En este caso hay uno solo: el encuentro en el desvío. |
|
paso 2 |
 |
0,3 km = 36 km/h . tE
|
[1] |
0,3 km = 0,18 km + vZ . tE
|
[2] |
|
|
paso 3 |
inevitablemente desembocás en un sistema de dos ecuaciones con dos incógnitas. Acá terminó la física del problema. Lo que queda es álgebra... estamos aprendiendo física. ¿Te lo resuelvo yo?
de la [1] despejamos tE y lo calculamos
tE = 0,00833 h (no te asustes, son sólo 30 segundos)
con ese valor vamos a la ecuación [2] y despejamos la velocidad de la zorra
vZ = (0,3 km – 0,18 km) / tE
|
|
paso 4
paso 5 |
| |
vZ = 14,4 km/h |
¡qué zorra! |
|
|
|
Ahora... si los empleados ferroviarios que van en la zorra necesitan 10 segundos como mínimo para hacer el cambio... ¿qué te parece que habrá que cambiar en las ecuaciones? ¡No sigas leyendo! Pensalo vos... ¡QUE NO SIGAS DIJE!
Ah, viste que lo podías sacar... lo que cambia es que, para la zorra, el instante de llegada al desvío -llamémoslo tD- será:
tD = tE – 10 s
Todo el resto no cambia... sólo en el último paso, así que lo hacemos rapidito... pasamos los 10 segundos a horas... a ver... creo que lo saco... pará, paso el 4, me llevo 1... son como... 0,00278 h |
|
|
| |
vZ´ = 21,6 km/h |
¡qué ferroviarios! |
|
|
|
| Los gráficos con cambio automático. |
Los gráficos con ferroviarios listos. |
|
|
|
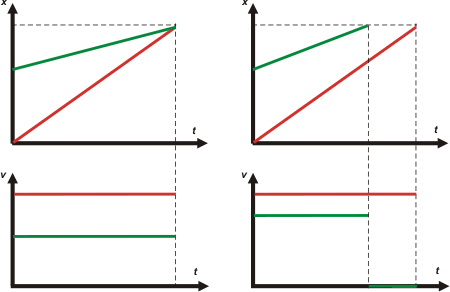 |
|
paso 6 |
| DESAFIO: Rehacé el problema pero trabajando todo en metros por minuto y tomando instante de tiempo inicial 15 minutos. Dale... parece absurdo pero es una buena ejercitación. |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
| | | |
|

